Redox reactions can be balanced with the half-reaction method. The half-reaction shows the oxidation and reduction processes separately.
For example,
Zn + Ag+ → Zn2+ + Ag
Follow these steps to balance this reaction:
1) Add the oxidation states and write the half-reactions. The oxidations states are only added to help identify the oxidation and reduction processes:
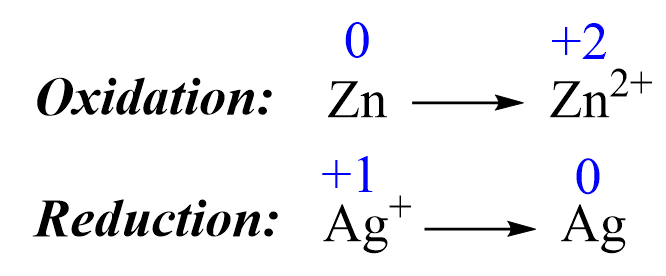
2) Balance the elements. In this case, they are balanced, so proceed to the next step.
3) Balance the charges by adding electrons:
Zn → Zn2+ + 2e–
1e– + Ag+ → Ag
4) Balance the number of electrons by multiplying the equation(s) with a whole number. The first equation has two electrons, and therefore, we multiply the second equation by two:
2 x [1e– + Ag+ → Ag] = 2e– + 2Ag+ → 2Ag
5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.
Zn → Zn2+ + 2e–
2e– + 2Ag+ → 2Ag
__________________
Zn + 2e– + 2Ag+ → 2Ag + Zn2+ + 2e–
6) Cancel any species that appear in equal quantitates on both sides of the equation:
Zn + 2e– + 2Ag+ → 2Ag + Zn2+ + 2e–
Zn + 2Ag+ → 2Ag + Zn2+
Balancing Redox Equations in Acidic Solution
In the example above, there are only two elements which simplifies balancing the reaction. There is an additional part to balancing redox reactions in acidic or basic conditions which results from the presence of oxygen and hydrogen atoms.
For example,
Fe2+ + Cr2O72- → Fe3+ + Cr3+
Do as we did in the previous example;
1) Add the oxidation states and write the half-reactions:
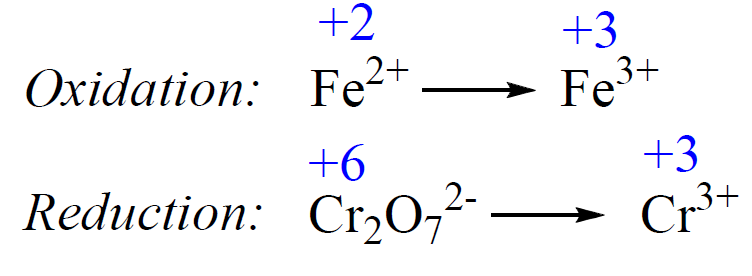
2) Balance the atoms. Add H2O to balance the O atoms, and H+ to balance the H atoms.
The atoms in the first half-reaction are balanced. For the second reaction, we need to equalize the Cr atoms, and add 7 H2O on the right side to balance the oxygen atoms:
Cr2O72- → 2Cr3+ + 7H2O
Now, to balance the H atoms, we need to add 14 H+ on the left side:
14H+ + Cr2O72- → 2Cr3+ + 7H2O
3) Balance the charges by adding electrons.
In the first equation, we add one electron on the right side:
Fe2+ → Fe3++ 1e–
In the second equation the charge is zero on the left side (+14 + (-7 x 2) = 0), we have +6 (+3 x 2) on the right side:
14H+ + Cr2O72- → 2Cr3+ + 7H2O
Therefore, add 6e– to balance the charges in the second equation:
6e– + 14H+ + Cr2O72- → 2Cr3+ + 7H2O
4) Balance the number of electrons by multiplying the equation(s) with a whole number. There are 6 e– in the second equation, so multiply the first equation by 6:
6 x [Fe2+ → Fe3++ 1e–] = 6Fe2+ → 6Fe3++ 6e–
5) Once everything is balanced, add the half-reactions together and cancel the electrons:
6Fe2+ → 6Fe3++ 6e–
6e– + 14H+ + Cr2O72- → 2Cr3+ + 7H2O
______________________________
6Fe2++ 14H+ + Cr2O72- → 6Fe3+ + 2Cr3+ + 7H2O
Check if everything is balanced. In this case, it is!
Balancing Redox Equations in Basic Solution
For reactions in basic solutions, we proceed all the way to balancing the equation as if it is in an acidic solution. At the end, for every H+, we add an equal number of OH– on both sides of the equation. A pair of H+ and OH– ions is then represented as a water molecule.
For example,
MnO4– + I– → MnO2 + I2
1) Write the half-reactions:
MnO4– → MnO2
I– → I2
2) Balance the atoms. Add H2O to balance the O atoms, and H+ to balance the H atoms.
The atoms in the first half-reaction are balanced.
For the first reaction, we need to equalize the oxygens, and therefore, we add 2 H2O on the right side:
MnO4– → MnO2 + 2H2O
And now, add 4 H+ on the left side to balance the hydrogens:
4H+ + MnO4– → MnO2 + 2H2O
For the second reaction, add 2 in front of I–:
2I– → I2
3) Balance the charges by adding electrons.
To balance the charges in the first equation, we add 3e– on the left side because there are three extra positive charges (+4 from the protons and -1 from the permanganate ion):
3e– + 4H+ + MnO4– → MnO2 + 2H2O
For the second equation, we need to add 2e– on the right side:
2I– → I2 + 2e–
4) Balance the number of electrons by multiplying the equation with whole numbers. There are 3 electrons in the first equation, and 2 electrons in the second, so ta balance this, we multiply the first equation by 2, and the second equation by 3:
2 x [3e– + 4H+ + MnO4– → MnO2 + 2H2O] = 6e– + 8H+ + 2MnO4– → 2MnO2 + 4H2O
3 x [2I– → I2 + 2e–] = 6I– → 3I2 + 6e–
5) Once everything is balanced, add the half-reactions together and cancel the electrons:
6e– + 8H+ + 2MnO4– → 2MnO2 + 4H2O
6I– → 3I2 + 6e–
__________________________________________________
8H+ + 2MnO4– + 6I– → 2MnO2 + 4H2O + 3I2
6) This is the balanced equation in acidic media, and one more step to make it in a basic media, is to add 8 OH– on both sides of the equation to get rid of the 8H+ ions on the left side. This works on the principle of combining H+ and OH– ions and representing it as water:
8OH– + 8H+ + 2MnO4– + 6I– → 2MnO2 + 4H2O + 3I2 + 8OH–
8H2O + 2MnO4– + 6I– → 2MnO2 + 4H2O + 3I2 + 8OH–
Notice that we now have 8 H2O on the left side, and only for on the right side. 4 H2O molecules on both sides cancel out, and we are left with the balanced equation in a basic media:
2MnO4– + 6I– + 4H2O → 2MnO2 + 3I2 + 8OH–
To summarize the balancing of redox reactions, remember that:
1) For reactions with only two elements, balance the atoms and then the charges by adding electrons where needed. Once the half-reactions are balanced, add them up and cancel any identical species that appear on both sides of the equation.
2) Balancing redox reactions in acidic media: Follow the same steps and remember, we add H2O to balance the O atoms, and H+ to balance the H atoms.
3) Balancing redox reactions in basic media: Follow the same steps as far balancing in acidic media and, in the end, add as many OH- ions as there are on either side of the equation. Convert an equal number of these ions to water, and cancel the water molecules on both sides of the equation.
Check Also
- Solutions
- Strong and Weak Electrolytes
- Dissociation of Ionic Compounds
- Molecular, Ionic, and Net Ionic Equations
- Molarity
- Dilution
- Ion Concentration
- Precipitation Reactions
- Definitions of Acids and Bases
- Acid-Base Reactions
- Stoichiometry of Reactions in Aqueous Solutions
- Acid-Base Titrations
- Oxidation State
- Oxidation-Reduction (Redox) Reactions
- Reactions in Aqueous Solutions Practice Problems
Practice
Balance the following redox reactions occurring in acidic aqueous solution:
a) Al(s) + Fe2+(aq) → Al3+(aq) + Fe(s)
b) SO32–(aq) + MnO4–(aq) → SO42–(aq) + Mn2+(aq)
c) Cr2O72- + C2O22- → Cr3+ + CO2
d) PbO2 + Mn2+ + SO42– → PbSO4 + MnO4–
e) MnO4−(aq) + H2O2(aq) → Mn2+(aq) + O2(g)
Balance the following redox reactions occurring in basic aqueous solution:
a) Mn2+ + ClO3– → MnO2 + ClO2
b) MnO4–(aq) + Br–(aq) → MnO2 + BrO3–(aq)
c) MnO4–(aq) + CN–(aq) → CNO-(aq) + MnO2(s)
d) H2O2(aq) + ClO2(aq) → ClO2–(aq) + O2(g)
e) MnO4–(aq) + Fe(OH)2(s) → MnO2(s) + Fe(OH)3(s)

I like your teaching method
THANKS for the examples
thank you for giving so many practice problems, they’ve been very helpful
Glad to hear that. Doing my best to make this as helpful as possible.