In the previous post, we talked about nuclear binding energy, and discussed a graph with important implications for the use of nuclear processes as sources of energy:
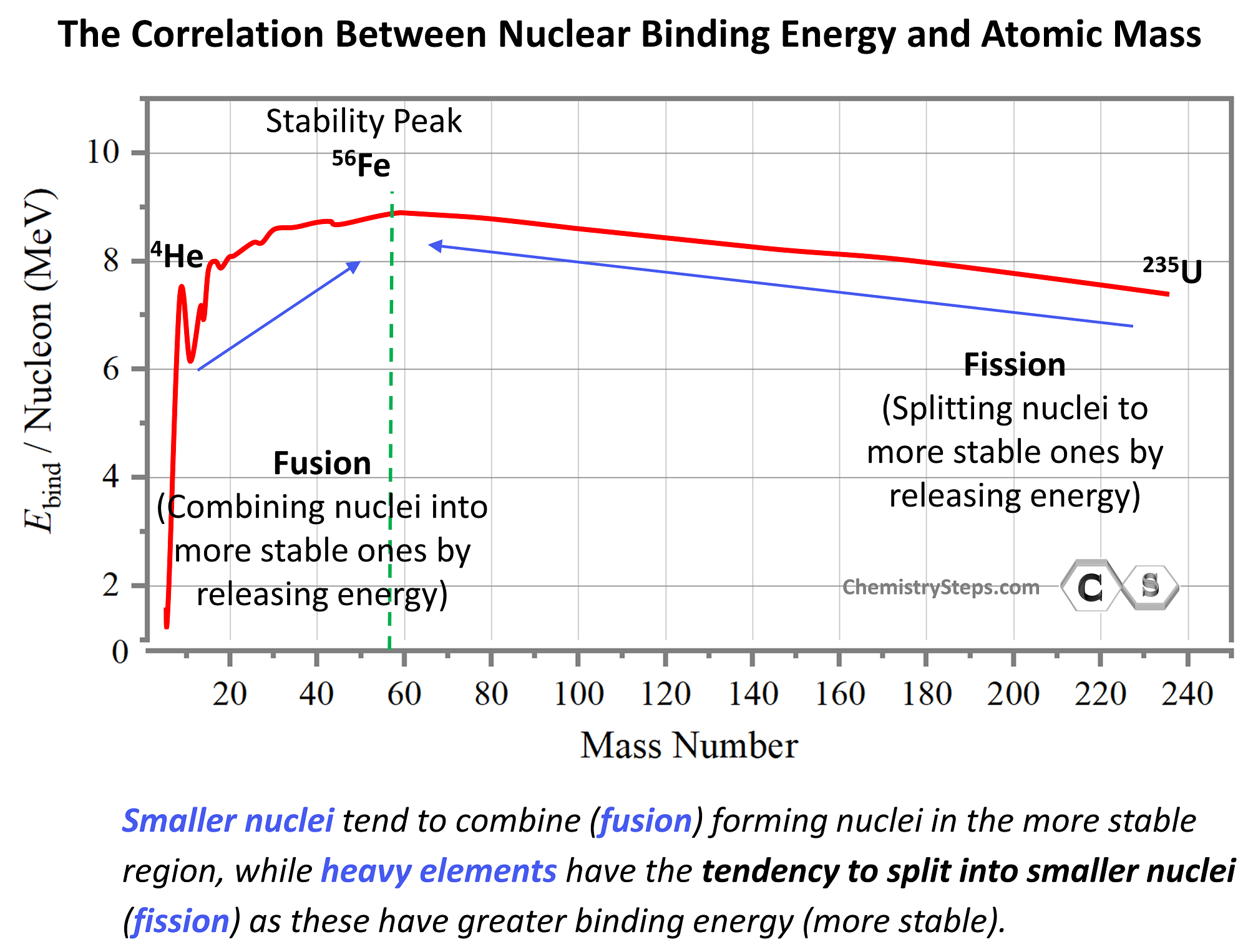
The key to predicting what types of nuclear reactions are going to be favorable based on the graph is that, like in any other process, the system tends to proceed in the direction that releases energy. In other words, the process where more sable products are formed shows the favorable direction.
The greater the binding energy per nucleon, the more stable the nuclide is, and the most stable elements are at the region of ~60 amu. The binding energy increases up to this region and then goes down as we move toward heavier elements. Based on this, we can see from the graph that smaller nuclei will tend to combine (fusion) forming nuclei in the more stable region, while heavy elements, being unstable, will have the tendency to split into smaller nuclei (fission) as these have greater binding energy (more stable).
This may seem counterintuitive by looking at the energy graph since fusion and fission appear to be going uphill. However, this is simply because the energy scale shows the energy needed to break nuclei rather than forming them. By mirroring the graph, we can show the energy released when a nucleus is formed, and in this case, the most stable nuclei will appear in the downhill region:
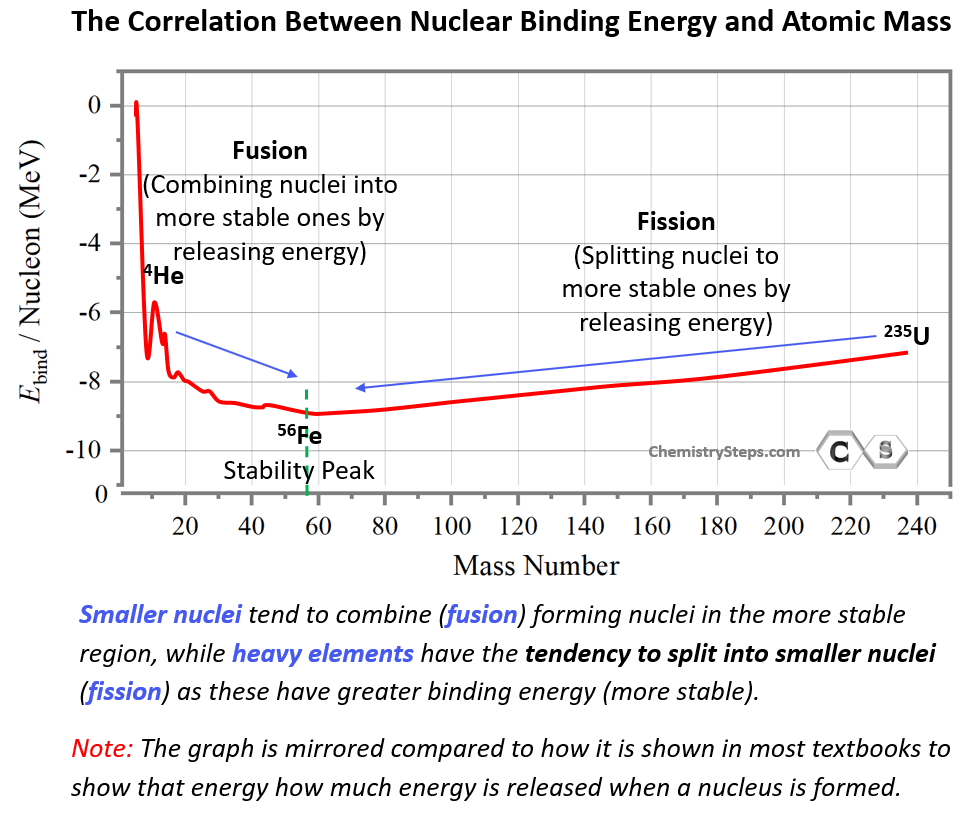
This may be a better way of comparing the stability of the nuclei as the most stable ones lower on the energy scale. In fact, some textbooks define nuclear binding energy as the one released when protons and neutrons come together to form a nucleus. These two are the reverse processes and conceptually there is no difference in how we formulate the nuclear binding energy. The analogy to this would be the bond dissociation energy vs the enthalpy of formation.
Nuclear Fission
Nuclear fission is a nuclear reaction where the nucleus, typically of a heavy element, is split into lighter nuclei. The representative example is perhaps the splitting of the uranium-235 isotope into Ba and Kr according to the following equation:
23592U + 10n→ 14056Ba + 9336Kr + 3 10n + Energy
The reaction was first performed in the mid-1930s by Enrico Fermi (1901–1954), in an attempt to synthesize a new element by bombarding the uranium isotope, the heaviest known element at that time, with neutrons. He intended to convert the uranium into a new element with an atomic number of 94 since the incorporated neutron would presumably undergo beta decay, converting a neutron into a proton.
Most nuclear fission reactions are highly exothermic because the forming smaller nuclei are more stable than the parent and therefore, energy is released when the reaction occurs.
Notice that this fission does not occur spontaneously even though it is energetically very favorable as the reaction is extremely exothermic. Just like we learned in kinetics and thermodynamics spontaneous reactions do not necessarily occur by themselves and a trigger to overcome the activation energy is needed.
The reaction releases 2.1 x 1013 J/mole of energy which is 26 million times larger than the combustion of methane. We have discussed this difference in more detail and calculated the mass difference in these representative reactions in the previous post, so feel fee to check that out as well.
Chain Reaction
Although we focused on the fact that fission produces new nuclides, it is also important to signify the formation of neutrons. Remember that the reaction was initiated by bombarding the parent nuclide with a neutron, and therefore, the neutrons produced during the fission can facilitate the splitting of other parent nuclides.
So, every neutron produced in the reaction triggers a new splitting making a chain reaction – the reaction is self-sustaining.

Now, not every neutron emitted during the reaction cause a new fission, and, if, on average, it is less than one neutron, the process stops, and the reaction is said to be subcritical. On the other hand, the process is said to be critical if it sustains itself at the same level which happens when exactly one neutron from each fission causes another fission event.
In many processes such as, for example, nuclear bombs, more than one neutron from each splitting causes another fission event. This situation is called supercritical as the process rapidly escalates causing a violent explosion.
This critical state can only be achieved if a certain mass of fissionable material, called the critical mass, is present in the reaction mixture.
For smaller samples, the chain reaction stops quickly as too many neutrons simply escape the material before hitting new nuclides.
Nuclear Fusion
Nuclear fusion is the combination of two light nuclei (below A = 60) to form a heavier one. Both in fission and fusion, the daughter nuclides have greater binding energies per nucleon than the parent nuclides, and therefore, they are energetically very favorable and extremely exothermic.
To keep the energetic aspect of nuclear fusion out of comparison, we should mention that an example of fusion is the reaction in the core of the Sun where hydrogen is being converted into helium. Although the process consists of several steps, overall, it takes four hydrogen atoms to fuse into each helium atom. During the process, some of the mass is converted into energy.
4 11H → 42He + 2 01β + Energy
Now, one may then wonder why we cannot use nuclear fusion reactions to generate energy. There is intense research to develop a feasible fusion process because, however, the major issue, we mentioned earlier, is the activation energy needed to facilitate these processes. The thing is that nuclear binding forces are extremely strong, but they are effective only at very small distances, and to bind, for example, two protons together and thereby release energy, they must first overcome the repelling electrostatic forces which requires extreme temperatures to provide the needed speed and kinetic energy.
Here is a 73-question, Multiple-Choice Quiz on Nuclear Chemistry:
Check Also

