Nuclear reactions are associated with enormous amounts of energy. For example, the energy coming from the sun is a result of a nuclear reaction, the devastating power of nuclear bombs is also the output of nuclear reactions.

So, what is the reason that nuclear reactions are so much more exothermic compared to, for example, conventional composition reactions?
The key difference and unique feature of nuclear reactions is that they are associated with significantly larger mass changes. Remember, in earlier chapters, and upcoming as well, including organic chemistry, we are going to rely on the law of conservation of mass, meaning the total mass of the reactants and products stays constant in chemical reactions.
This is a valid approximation because the mass change in chemical reactions is negligible, and we cannot even measure it using the balances in chemical laboratories. However, in nuclear reactions, the mass change is very important as it explains the huge energy changes associated with them.
So, what does the mass change have to do with the energy of chemical and nuclear reactions?
To understand this, we need to remember what Einstein said about their correlation in the theory of relativity. The theory of relativity tells us that the mass of an object is a measure of its energy in that the greater the mass of an object, the greater its energy. The famous equation proposed by Einstein is:
E = mc2
where E is the energy, m is the mass, and c is the speed of light (2.9979 x 108 m/s)
The implication of this equation is that mass and energy are equivalent and can be converted into one another, and this is what we are going to use to compare the mass and energy change of some chemical and nuclear reactions to see why nuclear reactions release or absorb so much energy.
For example, let’s see what the mass change during the combustion of methane (CH4) is.
Methane is the main component of natural gas, and we know that its combustion is a great source of energy (890.4 kJ/mol).
CH4 + 2O2 → CO2 + 2H2O, ΔH = 890.4 kJ
Rearranging Einstein’s equation, we can obtain the necessary expression for the mass change:
ΔE = (Δm)c2
\[{\rm{\Delta }}m\; = \,\frac{{{\rm{\Delta }}E}}{{{c^2}}}\]
Before plugging in the numbers, we need to express the 890.4 kJ in kg⋅m2⋅s−2. One Joule is equivalent to 1 kg⋅m2⋅s−2, so, we can write that 1 J = 1 kg⋅m2⋅s−2, and therefore, 890.4 kJ = 8.904 x 105 kg⋅m2⋅s−2.
\[{\rm{\Delta }}m\; = \,\frac{{{\rm{ – 8}}{\rm{.904}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{5}}}\,{\rm{kg \times }}\cancel{{{{\rm{m}}^{\rm{2}}}{\rm{ \times }}{{\rm{s}}^{{\rm{ – 2}}}}}}}}{{{{\left( {{\rm{3}}{\rm{.00}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{8}}}\,\cancel{{{\rm{m/s}}}}} \right)}^{\cancel{{\rm{2}}}}}}}\, = \, – 9.9\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 12}}}}{\rm{ kg}}\;{\rm{ = }}\, – 9.9\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 9}}}}{\rm{ g}}\]
The negative sign indicates that burning 1 mol of methane results in a decrease of mass by 9.9 x 10-9 g. What is more important here is that you need to remember that if the mass decreases, then the process must release energy, and if the mass increases, then the system must have absorbed energy. In other words, this 9.9 x 10-9 g do not just vanish, but they are interconverted into the equivalent amount of energy that is released by the system.
So now, let’s see how much the mass changes during a typical nuclear reaction. For example, the 23892U isotope undergoes an alpha decay producing 23490Th according to this equation:
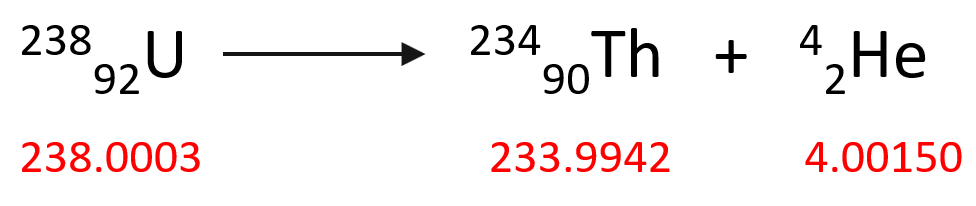
To calculate the mass change of this reaction, we need to subtract the sum of the mass of the starting material (23892U isotope) from the products (23490Th and 42He).
Remember:
Δm = Σ m (products) – Σ m (reactants)
The exact atomic masses can usually be found in the corresponding appendix of your textbook, and since they are already given here, let’s enter the numbers in the expression for Δm:
Δm = m (23490Th) + m (42He) – m (23892U)
Δm = (233.9942 + 4.00150 – 238.0003) amu = -0.0046 amu
The change of the mass for a one-mole sample of 23892U will then be the same number expressed in grams:
Δm = (233.9942 + 4.00150 – 238.0003) g = -0.0046 g
Compare this to the mass change during the combustion of methane (9.9 x 10-9 g). That is about 465,000 times larger and that is how much more energy is going to be released in this reaction.
Let’s calculate the energy using the Einstein’s equation:
ΔE = (Δm)c2
Before adding the numbers, we will convert the grams to kilograms to match the SI units of mass and Joule (kg⋅m2⋅s−2):
ΔE = -0.0046 x 10-3 kg x (3.00 x 108 m/s)2
ΔE = -4.14 x 1014 kg⋅m2⋅s−2 = -4.14 x 1011 J = -4.14 x 108 kJ
Just to double-check, we can divide this by the energy change of the combustion of methane:
ΔE2/ ΔE1 = -4.14 x 108 kJ : 890.4 kJ = 465,000
As expected, we got the same magnitude by simply comparing the mass changes of the two reactions since, for both cases, we multiply mass by the square of the speed of light.
The reason that the interconversion of mass and energy in chemical reactions is not important, and the mass changes are negligible is that the energy changes involved in breaking or forming chemical bonds are a lot smaller compared to the binding forces between the protons and neutrons.
The energy associated with nuclear reactions is explained by the nuclear binding energy which we will cover in the next article.
Electrons in Nuclear Reactions
One thing I wanted to mention here is the mass of the electrons. The term binding energy refers to the nucleus, and therefore, the mass difference is between the mass of the nucleus and the total mass of the protons and neutrons. Most tables give the atomic masses, and to find the mass o the nucleus, we need to subtract the mass of the electrons in the atom:
m (nulceus) = m (atom) – m (electrons)
Now, since the total number of electrons does not change, we do not need to subtract the total mass of electrons from the mass of each atom in order to obtain the nuclidic mass (the mass of the nucleus). In other words, the masses of electrons will cancel out and therefore, the overall change in mass will be the same in either case. That is the difference will be the same whether we use the atomic masses or the nuclidic masses which are obtained by subtracting the mass of electrons. This simply makes the calculations easier because most tables provide the atomic mass rather than the mass of the nucleus.
This, however, gets trickier in processes such as beta decay and positron emission because the number of electrons in the atoms changes.
We will discuss this in the next article devoted to nuclear-binding energy which is the energy changes associated with forming nuclei from protons and neutrons as well as the revere process of breaking nuclei into its component particles.
To summarize, the main lesson you want to remember from this post is that mass interconverts into energy and vice versa. If the reaction is associated with loss of mass, then it will release energy equivalent to the that mass change. If the reaction, or the system, gains mass, then there must be an energy input.
Now, going back to the question of why nuclear reactions are associated with such large amounts of energy, remember the reason for this is that the mass changes during nuclear reactions are significantly larger.
Here is a 73-question, Multiple-Choice Quiz on Nuclear Chemistry:
Check Also

