What is the Nernst Equation Used For?

Nernst equation is used to calculate the cell potential under nonstandard conditions based on E^o_cell and the log of the reaction quotient.

where E^o is the cell potential under standard conditions, n is the moles of the electrons in the half-reactions, and Q is the reaction quotient

Another version of the equation is when the natural logarithm of the Q is used:

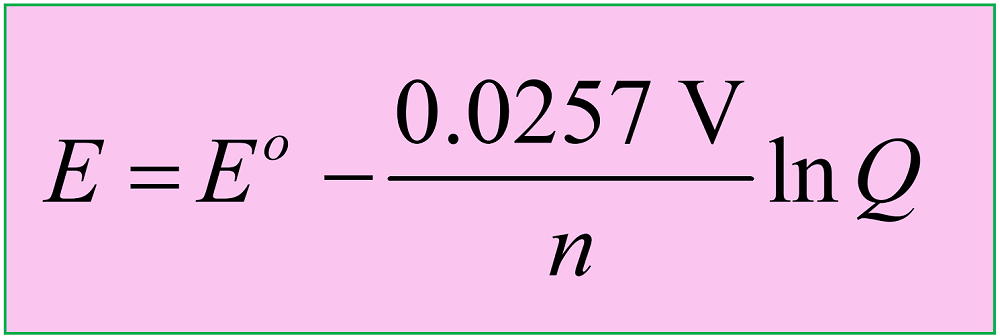
Both equations are applicable to reactions carried out at 25 ^oC (298 K), so let’s why is that the case, and how the equation is derived before looking at some examples. 

Deriving the Nernst Equation

There are two equations we need to remember to derive the Nernst equation. One is the equation correlating the Gibbs free energy change under standard (ΔG°) and nonstandard conditions(ΔG)  , and the reaction quotient (Q):

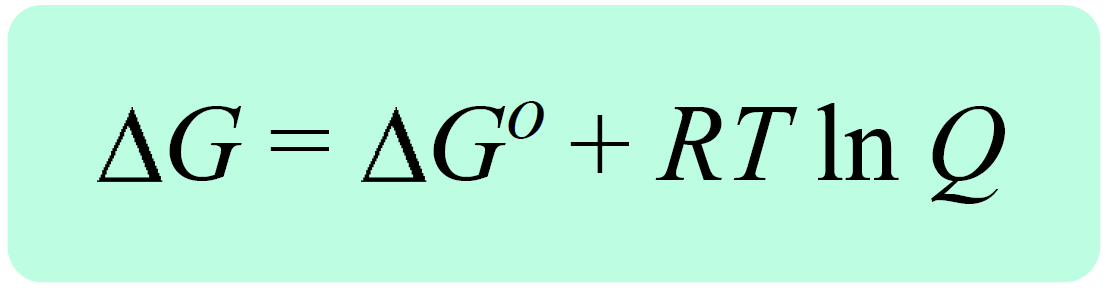
where ΔG is the free-energy change under nonstandard-state conditions, ΔG° is the free-energy change under standard-state conditions, R is the gas constant, T is the temperature in kelvin, and Q is the reaction quotient

We talked about this equation in detail here, so feel free to check it out before going forward.

The second equation is the correlation between the change in Gibbs free energy and the cell potential:

ΔG° = –nFE°_cell, ΔG = –nFE_cell

Combing these two equations, we can write that:

–nFE_{cell =} –nFE°_cell + RTln Q

To simplify the equation, we divide each side by –nF which leads to the Nernst equation:

\[E\; = \,{E^o}\; – \,\frac{{RT}}{{nF}}\,\ln \,Q\]

Switching from the natural log, we can also write it as:

\[E\; = \,{E^o}\; – \,\frac{{2.303RT}}{{nF}}\,\log \,Q\]

E is the cell potential in the given nonstandard condition, E^o is the cell potential at standard conditions, n is the moles (coefficient) of electrons in the half-reactions, F is the Faraday constant (96,485 coulombs/mol e^_) and it is equivalent to the charge on one mole of electrons, R is the universal gas constant (8.314 J / mol·K), and Q is the reaction quotient

Notice that all the parameters in the formula are constant except for the temperature, and if we apply the equation to a reaction carried out at 298 K, we can get the most common ways of the Nernst equation:

\[E\; = \,{E^o}\; – \,2.303\, \times \,\frac{{8.314\,\frac{{\cancel{{\rm{J}}}}}{{\cancel{{{\rm{mol}}\,{\rm{K}}}}}}\; \times \;298.15\;\cancel{{\rm{K}}}}}{{\frac{{{\rm{n}}\;\cancel{{{\rm{mol}}\;{{\rm{e}}^{\rm{ – }}}}}}}{{\cancel{{{\rm{mol}}}}\,}}\;\left( {96,485\frac{{\cancel{{\rm{J}}}}}{{{\rm{V}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}\,}}} \right)}}\,\log \,Q\]

The Correlation Between E_cell and Q

Looking at the Nernst equation for reactions at 25 ^oC, we can see that the cell potential under nonstandard conditions differs from the one under standard conditions, only based on the quotient.

Remember, Q has the same expression as the equilibrium constant and the only difference is that we use the given concentrations rather than the ones at the equilibrium:

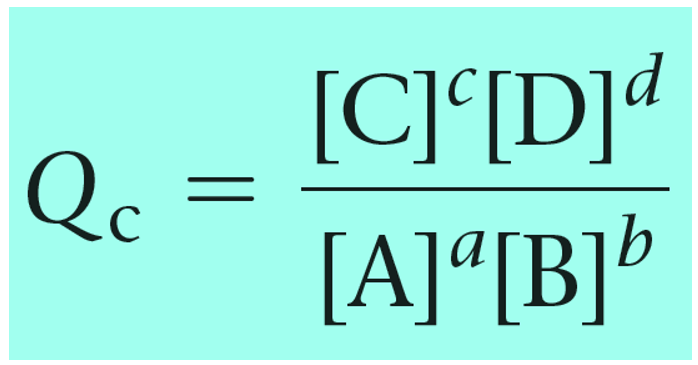
Reaction quotient, Q tells us whether the forward or reverse reactions are going to be favorable based on the given concentrations of the reactants and products. The driving force here is that the system always tries to reach an equilibrium where Q becomes equal to the K:

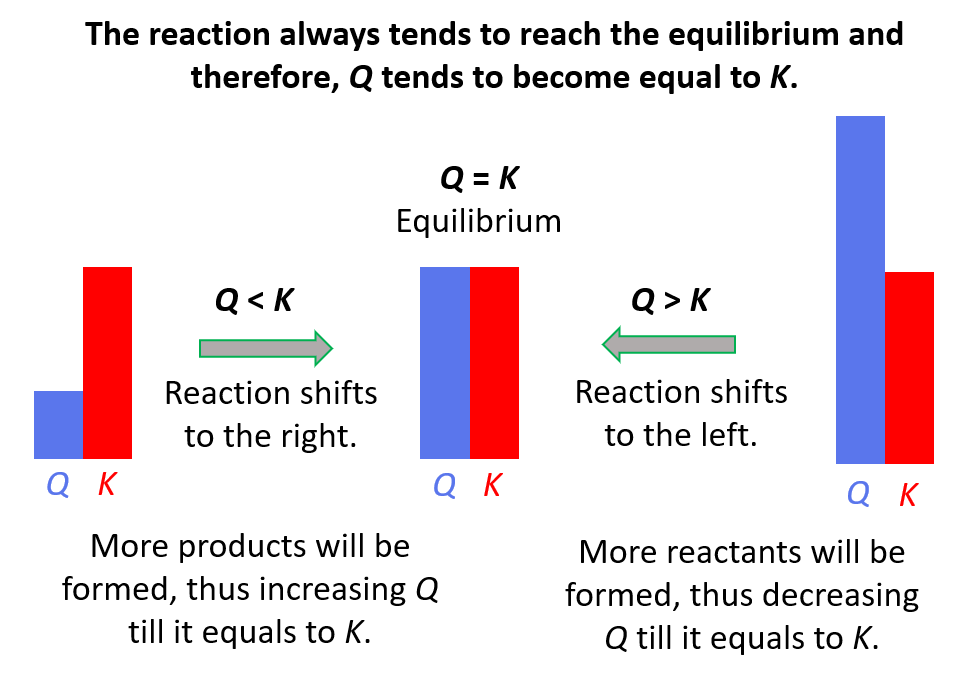
Feel free to review the concept of reaction quotient and equilibrium constant by clicking on the highlighted sections, but here is the summary of what we need to know about Q and the direction of the equilibrium:

• Q < K Reaction tends to form more products.
• Q > K Reaction tends to form more reactants.
• Q = K Reaction is already at equilibrium.

Applying this to the Nernst equation, we can write the following correlations between the cell potential and the reaction quotient:

• When Q < 1, it means [reactant] > [product], ln Q < 0, so E_cell > E°_cell.
• When Q = 1, it means [reactant] = [product], ln Q = 0, so E_cell = E°_cell.
• When Q > 1, it means [reactant] < [product], ln Q > 0, so E_cell < E°_cell.
• When Q = K, it means [product] >> [reactant], ln Q = E°_cell, so E_cell = 0 .

So, we can divide the operation of the cell into four stages:

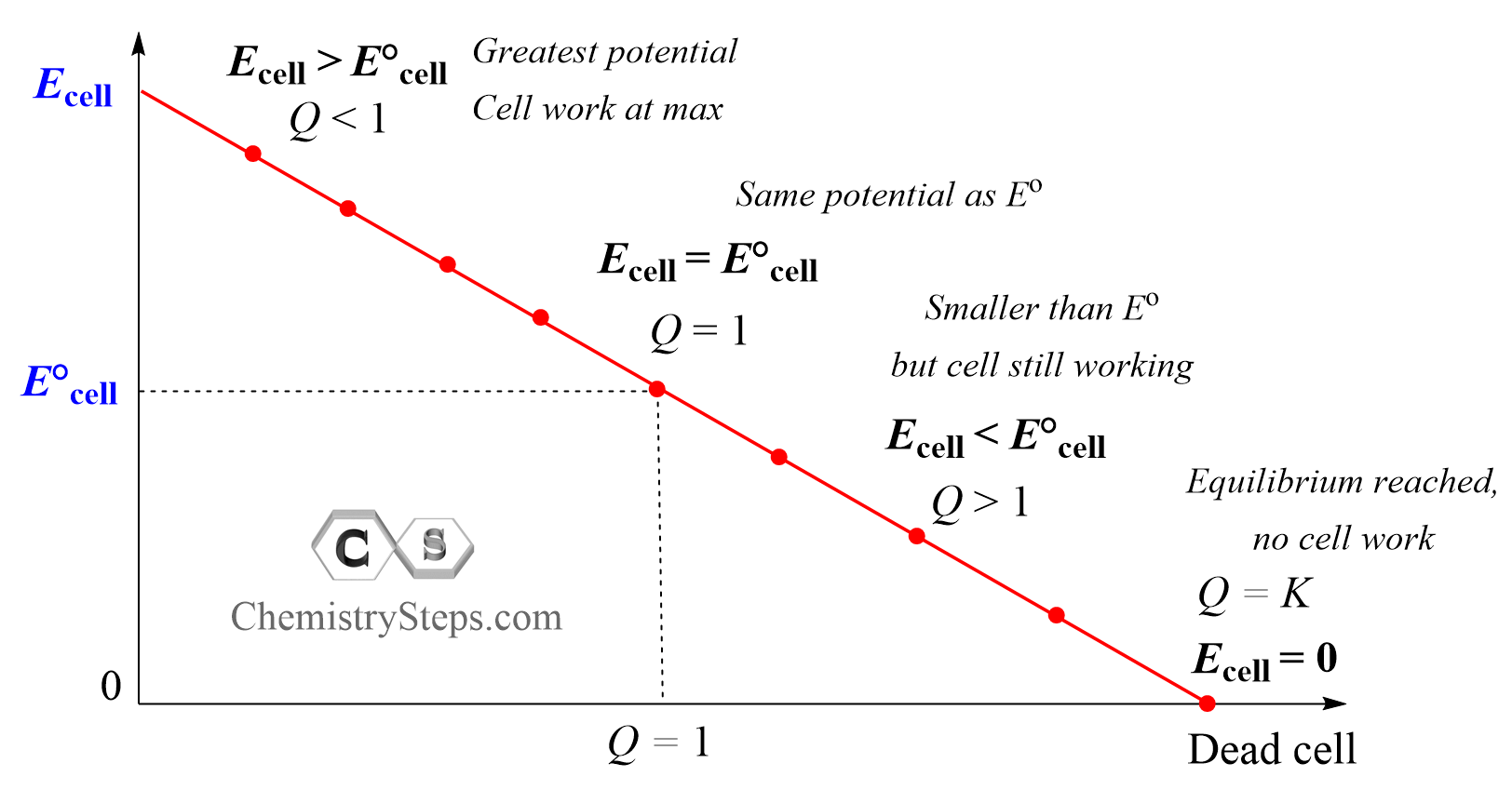
When the Q < 1, it means there is more of the reactants than products, and according to Le Châtelier’s principle, the reaction is going to have a greater tendency to shift forward to form more of the products. This, in turn, means the overall cell potential, at the given concentrations, is greater than the cell potential under standard conditions (E_cell > E°_cell).

At some point, as the concentration of the products is increasing and that of the reactants is decreasing, Q equals, the log term is zero, and the cell potential is the same as it would be under standard conditions: E_cell = E°_cell as Q = 1, and log 1 = 0.

As the reaction continues, Q becomes larger than 1, Q > 1, because there is more product than reactant in the system, resulting in a smaller cell potential compared to that of under standard conditions (E_cell < E°_cell). The reaction is still occurring, however, because of the smaller potential, it can do less work. Finally, when Q equals K, an equilibrium is reached and E_cell becomes zero which means the cell is dead and no more work can be done. 

What Goes in the Expression of Q?

Remember, we do not include the liquids and solids, even when they are the electrodes, in the expression for Q as it only contains those species with concentrations (and/or pressures) that can change during the reaction.

For example, in the reaction between manganese and lead ion, the Mn and Pb electrodes do not appear in the expression for Q:

Mn(s) + Pb²⁺(aq) → Mn²⁺(aq) + Pb(s) 

\[E\; = \,{E^o}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[M}}{{\rm{n}}^{{\rm{2 + }}}}{\rm{]}}}}{{{\rm{[P}}{{\rm{b}}^{{\rm{2 + }}}}{\rm{]}}}}\]

Nernst Equation – Examples

A voltaic cell runs the following redox reaction:

Sn²⁺(aq) + Mg(s) → Sn(s) + Mg²⁺(aq)

a) For each concentration set, determine, without using the Nernst equation, whether E_cell is larger or smaller than E°_cell and b) Calculate the E_cell:

1) when [Sn²⁺] = 1.0 Mand [Mg²⁺] = 2.5 M

2) when [Sn²⁺] = 3.0 Mand [Mg²⁺] = 1.0 M

1) [Sn²⁺] = 1.0 Mand [Mg²⁺] = 2.5 M

For part (a) 

To estimate if E_cell is larger or smaller than E^o_cell, we need to look at the reaction quotient.

The concentration of the product, Mg²⁺ is higher than that of Sn²⁺ and therefore, according to the Le Chatelier’s principle, the tendency of the forward reaction will be less than at standard conditions since Q > 1.

\[Q\, = \,\frac{{[{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}]}}{{[{\rm{S}}{{\rm{n}}^{{\rm{2 + }}}}]}}\, = \,\frac{{2.5}}{1}\, = \,2.5\]

This also means that E_cell is smaller than E°_cell. Remember the pattern: if Q > 1, E_cell < E°_cell, and if Q < 1, E_cell > E°_cell. 

Part (b). To confirm this assessment, we need to use the Nernst equation and calculate E_cell.

\[E\; = \,{E^o}\; – \,\frac{{0.0257\;{\rm{V}}}}{n}\,\ln \,Q\]

Remember, V is just a unit here, and if it confuses you, you can write the equation as:

\[E\; = \,{E^o}\; – \,\frac{{0.0257}}{n}\,\ln \,Q\]

First, calculate the E°_cell by writing the half-reactions and looking up each cell potential. We have a separate post on calculating the cell potential at standard conditions so feel free to check that for more details.

Sn²⁺(aq) + 2e^– → Sn(s)    E^o = -0.14 V

Mg(s) → Mg²⁺(aq) + 2e^–  E^o = +2.37 V

E^o_cell = -0.14 V + 2.37 V = 2.23 V

And know, we can plug the numbers into the Nernst equation and determine the E_cell:

\[E\; = \,{E^o}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[M}}{{\rm{g}}^{{\rm{2 + }}}}{\rm{]}}}}{{{\rm{[S}}{{\rm{n}}^{{\rm{2 + }}}}{\rm{]}}}}\]

\[E\; = \,2.23\,{\rm{V}}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[2}}{\rm{.5]}}}}{{{\rm{[1}}{\rm{.0]}}}}\; = \;2.218\,{\rm{V}}\]

Because Q = 2.5, the difference between E_cell and E°_cell is not very large due to the logarithm. So, at this concentration ratio, the cell potential is smaller than E°_cell, however, the reaction is still spontaneous and will proceed forward until an equilibrium is reached when Q = K and E_cell = 0. 

2) [Sn²⁺] = 3.0 M and [Mg²⁺] = 1.0 M

Part (a)

There is more reactant than product in the system, so the reaction will tend to shift forward more than it would under standard conditions. Therefore, E_cell should be larger than E°_cell: Q < 1, E_cell > E°_cell. 

Part (b)         

We have already determined the E°_cell, so we can use it in the Nernst equation to calculate the E_cell:       

\[E\; = {\mkern 1mu} {E^o}\; – {\mkern 1mu} \frac{{{\rm{0}}.{\rm{0257}}\;{\rm{V}}}}{{\rm{2}}}{\mkern 1mu} {\rm{ln}}{\mkern 1mu} \frac{{[{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}]}}{{[{\rm{S}}{{\rm{n}}^{{\rm{2 + }}}}]}}\]

\[E\; = \,2.23\,{\rm{V}}\; – \,\frac{{{\rm{0}}{\rm{.0257}}\;{\rm{V}}}}{{\rm{2}}}\,{\rm{ln}}\,\frac{{{\rm{[1]}}}}{{{\rm{[3}}{\rm{.0]}}}}\; = \;2.244\,{\rm{V}}\]

Check Also

• Balancing Redox Reactions
• Galvanic Cells
• How to Calculate Standard Cell Potential
• The Correlation Between E^o_cell, ΔG°, and K
• Nernst Equation Practice Problems
• Concentration Cells
• Electrolytic Cells
• Electrolysis
• Electrolysis of Water
• Calculating the Mass of Metal in Electroplating
• Cell Potential Practice Problems
• E^o, ΔG^o, K – Practice Problems
• Electrochemistry Practice Problems