We have seen, in this chapter, that a positive standard cell potential (E°_cell) indicates a spontaneous electrochemical reaction, and a negative sign corresponds to a nonspontaneous reaction.

Now, recall from thermodynamics that we always referred to the Gibbs free energy for determining whether a process is spontaneous or not. This means E°_cell and ΔG° must be related and one key difference is their signs. Unlike the cell potential, a negative value of the ΔG indicates a spontaneous reaction.

ΔG° ∞ –E^o_cell

The actual relationship between the free energy change and the cell potential is given by the following formula:

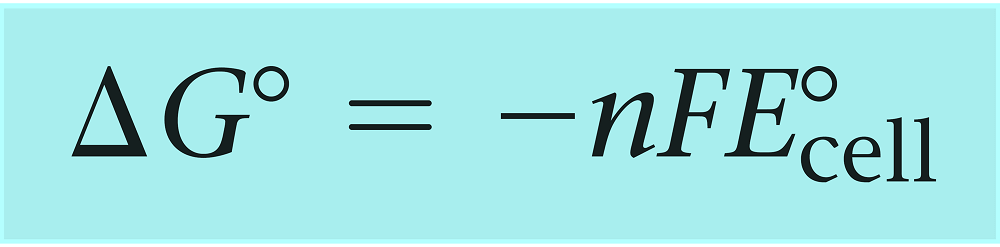
where n is the number of moles of electrons transferred in the reaction and F is the Faraday constant (96,485 coulombs/mol e^_) and it is equivalent to the charge on one mole of electrons

For a reaction carryout out under nonstandard conditions, we will have: ΔG = –nFE_cell

Now, the cell potential is most often going to be in volts, and therefore, you will also need to know the conversion between coulombs (C) and volts (V): 1 J = 1 C · 1 V.

Example: Use tabulated electrode potentials to calculate ΔG°_rxn for the following reaction at 25 °C.

Zn(s) + Cu²⁺(aq) → Zn²⁺(aq) + Cu(s)

The plan: We will first calculate the cell potential and then use it to determine the ΔG°. Check this article for the details about calculating the cell potential at standard conditions.

Solution:

1) Separate the half-reactions to calculate the cell potential:

Zn(s) → Zn²⁺(aq) + 2e^–  E^o = +0.76 V

Cu²⁺(aq) + 2e^– → Cu(s) E^o = +0.34 V

E^o_cell = +0.76 V + (+0.34 V) = 1.10 V

Once again, what we did here is looked up the values of E^o and changed the sign of E^o for the reaction that is reversed. In this case, it is the oxidation of Zn. The E^o (Zn²⁺ → Zn(s)) is -0.76 V and because we have the reverse reaction, we changed the sign and simply added the E^o values to find the cell potential. This method seemed to be less confusing to my students, and that is how will do in these practice problems. Feel free to check this article for more information.

2) Now that we have the value of E^o_cell, we can use in the formula for ΔG°:

ΔG° = –nFE^o_cell

\[\Delta G^\circ {\rm{ }} = {\rm{ }} – nF{E^o}_{cell}\; = \, – 2\,\cancel{{{\rm{mol }}{{\rm{e}}^{\rm{ – }}}}}\,{\rm{ \times }}\,\frac{{{\rm{96,485}}\,{\rm{C}}}}{{\cancel{{{\rm{mol }}{{\rm{e}}^{\rm{ – }}}}}}}\;{\rm{ \times }}\,{\rm{1}}{\rm{.10}}\,{\rm{V}}\,{\rm{ = }}\, – {\rm{2}}\;{\rm{ \times }}\,{\rm{96,485}}\,\cancel{{\rm{C}}}\,{\rm{ \times }}\,{\rm{1}}{\rm{.10}}\frac{{\rm{J}}}{{\cancel{{\rm{C}}}}}\,{\rm{ = }}\, – 2.12\,{\rm{ \times }}\,{10^5}\,{\rm{J}}\,{\rm{ = }}\, – 2.12\,{\rm{ \times }}\,{10^2}\,{\rm{kJ}}\]

As expected for a spontaneous reaction, the cell potential is positive while the ΔG° is a negative number.

The Relationship between E°_cell and K

Another important correlation in electrochemistry is the one between the cell potential and equilibrium constant. This is still going to be through the Gibbs free energy change as, remember, it is correlated with the equilibrium constant through the following formula:

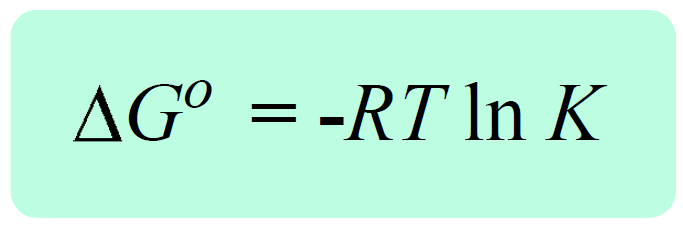
By substituting ΔG° with –nFE^o_cell, we can write the following equation:

–nFE^o_cell = –RT ln K

Dividing both sides by –nF, we obtain a new formula for the E^o_cell:

\[{E^o}_{{\rm{cell}}}\; = \,\frac{{RT}}{{nF}}\,\ln \,K\]

Where E^o_cell is the cell potential at standard conditions, n is the moles (coefficient) of electrons in the half-reactions, F is the Faraday constant (96,485 coulombs/mol e^_) and it is equivalent to the charge on one mole of electrons, R is the universal gas or energy constant (8.314 J / mol·K), and K is the equilibrium constant

Notice that all the parameters in the formula are constant except for the temperature, and if we apply the equation to a reaction carried out at 298 K, we can get a simplified and more common equation:

\[{E^o}\; = \,\,\frac{{8.314\,\frac{{\cancel{{\rm{J}}}}}{{\cancel{{{\rm{mol}}\,{\rm{K}}}}}}\; \times \;298.15\;\cancel{{\rm{K}}}}}{{\frac{{{\rm{n}}\;\cancel{{{\rm{mol}}\;{{\rm{e}}^{\rm{ – }}}}}}}{{\cancel{{{\rm{mol}}}}\,}}\;\left( {96,485\frac{{\cancel{{\rm{J}}}}}{{{\rm{V}}\,\cancel{{{\rm{mol}}\,{{\rm{e}}^{\rm{ – }}}}}\,}}} \right)}}\,\ln \,K\]

\[{E^o}_{{\rm{cell}}}\; = \,\frac{{0.0257\;{\rm{V}}}}{n}\,{\rm{ln}}\,K\]

Alternatively, we can also use the equation based on log considering that ln K = 2.303 log K:

\[{E^o}_{{\rm{cell}}}\; = \,\frac{{0.0592\;{\rm{V}}}}{n}\,{\rm{log}}\,K\]

So, keep these formulas in mind or handy when solving problems related to E^o_cell and K:

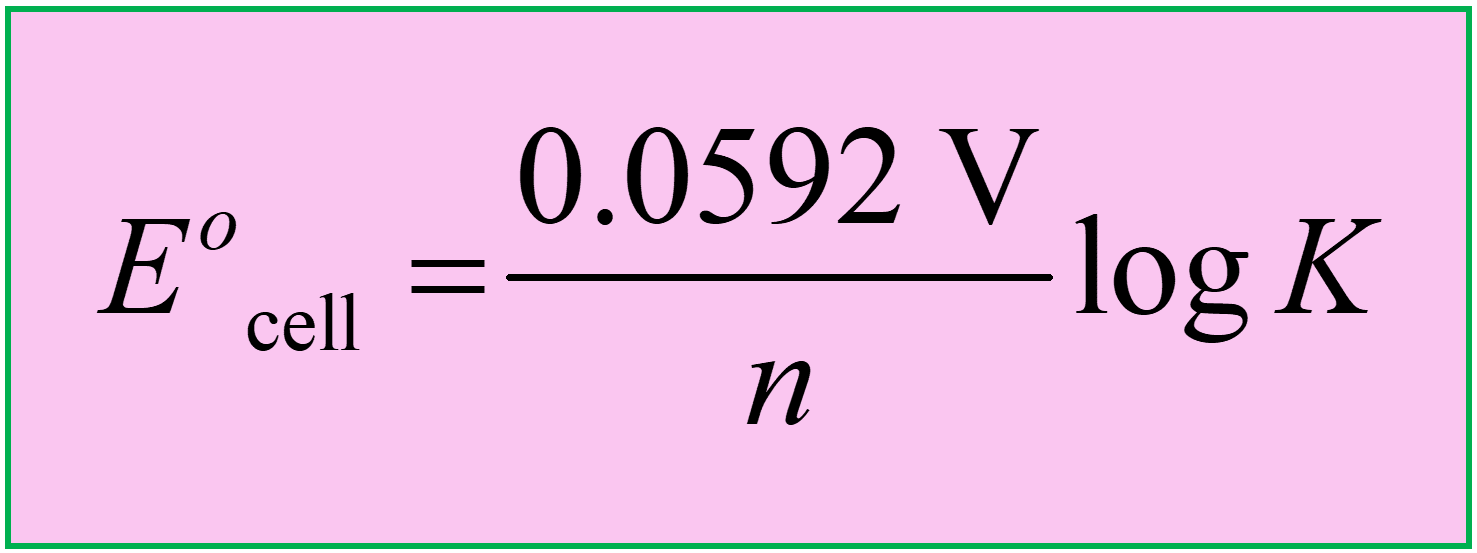
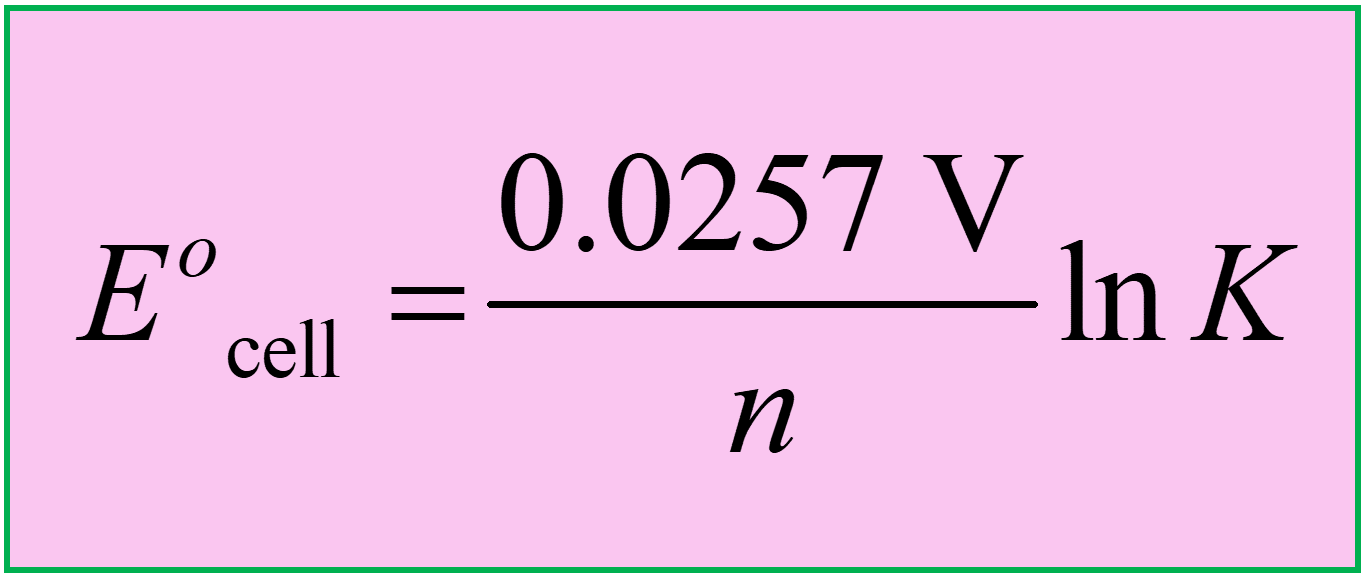
Now, how can we interpret these equations? The first thing to see here is that when the reaction is spontaneous (E°_cell > 0), K > 1 as the equilibrium lies towards the forward reaction. Notice also that the magnitude of K increases exponentially with E°_cell, and therefore, a reaction with a large positive E°_cell has K >> 1. Consequently, for a reaction with a large negative E°_cell, we expect to have K << 1.

When the cell potential is negative (E°_cell < 0), then the reaction is not spontaneous and the equilibrium lies to the left, meaning the reverse reaction is favorable and thus K < 1.

And finally, when E°_cell = 0, an equilibrium is established, and K = 1.

These trends and the key equations correlating are summarized for you in the following chart:

These correlations of the standard cell potential bring a very useful application of being able to calculate the equilibrium constants from electrochemical data. Remember, that we can calculate the ΔG° using the standard free energies of formations, or ΔH° and ΔS° however, the advantage here is that we have a direct experimental method for determining K and ΔG° by measuring E^o_cell, especially for reactions where ΔH° and ΔS° are not given.

Example: Calculate the ΔG°_rxn and equilibrium constant and for the following reaction carried out under standard conditions.  

Sn²⁺(aq) + Mg(s) → Sn(s) + Mg²⁺(aq)

Solution – Part A: ΔG° is correlated to E^o_cell with the following formula:

ΔG° = –nFE^o_cell

Therefore, the plan is to first calculate the cell potential and then use it to determine the ΔG°.

1) Separate the half-reactions, and switch the sign of E^o for the reversed reaction:

Sn²⁺(aq) + 2e^– → Sn(s)    E^o = -0.14 V

Mg(s) → Mg²⁺(aq) + 2e^–  E^o = +2.37 V

2) Calculate the E^o_cell by adding the potentials of the two reactions:

E^o_cell = -0.14 V + 2.37 V = 2.23 V

3) Use the value of E^o_cell to determine the ΔG°:

ΔG° = –nFE^o_cell

\[\Delta G^\circ {\rm{ }} = {\rm{ }} – nF{E^o}_{cell}\; = \, – 2\,\cancel{{{\rm{mol }}{{\rm{e}}^{\rm{ – }}}}}\,{\rm{ \times }}\,\frac{{{\rm{96,485}}\,{\rm{C}}}}{{\cancel{{{\rm{mol }}{{\rm{e}}^{\rm{ – }}}}}}}\;{\rm{ \times }}\,{\rm{2}}{\rm{.23}}\,{\rm{V}}\,{\rm{ = }}\, – {\rm{2}}\;{\rm{ \times }}\,{\rm{96,485}}\,\cancel{{\rm{C}}}\,{\rm{ \times }}\,{\rm{2}}{\rm{.23}}\frac{{\rm{J}}}{{\cancel{{\rm{C}}}}}\,{\rm{ = }}\, – 4.30\,{\rm{ \times }}\,{10^5}\,{\rm{J}}\,{\rm{ = }}\, – 430\,{\rm{kJ}}\]

Solution – Part B: Calculating the equilibrium constant.

The equation we need is:

\[{E^o}_{{\rm{cell}}}\; = \,\frac{{0.0257\;{\rm{V}}}}{n}\,{\rm{ln}}\,K\]

Dividing both sides of the equation by 0.0257 V/n, we get an expression for ln K:

\[{\rm{ln}}\,K\, = \,\frac{{n{E^o}_{{\rm{cell}}}}}{{0.0257}}\,\]

From here, we get rid of the ln by raising e to the power of nE^o/0.0257:

\[K\, = \,{e^{\frac{{n{E^o}_{{\rm{cell}}}}}{{0.0257}}\,}}\]

We have determined in part A that E^o_cell = 2.23 V, so all we need now is plugging the numbers:

\[K\; = \;{e^{\frac{{2\, \cdot \,2.23}}{{0.0257}}}}\, = \;2.33\, \times \,{10^{75}}\]

As expected, we have a spontaneous process confirmed by a positive E^o_cell, a negative ΔG°, K>>1.

Check Also

• Balancing Redox Reactions
• Galvanic Cells
• How to Calculate Standard Cell Potential
• Nernst Equation
• Nernst Equation Practice Problems
• Concentration Cells
• Electrolytic Cells
• Electrolysis
• Electrolysis of Water
• Calculating the Mass of Metal in Electroplating
• Cell Potential Practice Problems
• E^o, ΔG^o, K – Practice Problems
• Electrochemistry Practice Problems