The Henderson–Hasselbalch equation relates the pH of a buffer solution to the initial concentration of its components.
Let’s say we have a buffer containing the generic weak acid HA and its conjugate base A–. The dissociation of the acid can be shown as:
HA(aq) + H2O(l ) ⇆ H3O+(aq) + A–(aq)
The Henderson–Hasselbalch equation for this system can be shown as:
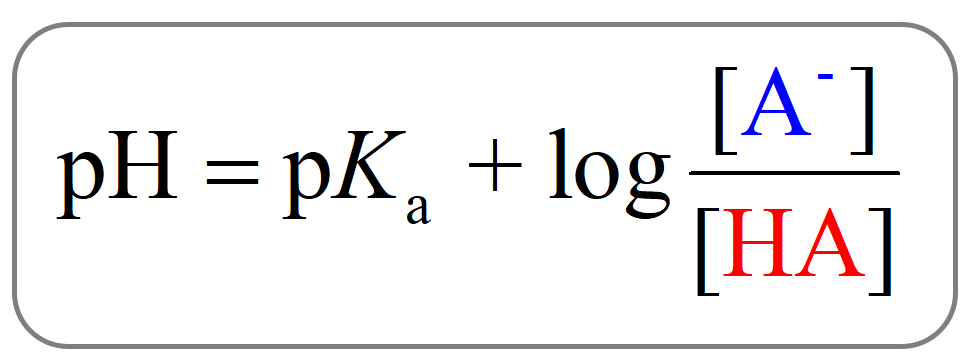
Where [HA] is the concentration of the acid and [A–] is the concentration of its conjugate base.
For example, if we make a buffer solution containing 0.400 M acetic acid (CH3COOH) and 0.250 M of its conjugate base CH3CO2Na, the pH of the buffer can be calculated by simply using these initial concentrations and the Ka of the acid:
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HA]}}}}\;\]
\[{\rm{pH}}\; = \;4.75\; + \,{\rm{log}}\frac{{{\rm{0}}{\rm{.250}}\;\cancel{M}}}{{{\rm{0}}{\rm{.400}}\;\cancel{M}}}\; = \,4.55\]
This approach for calculating the pH of a buffer solution is shorter than the equilibrium approach, however, it only yields accurate results if (a) the initial concentrations of the buffer components are sufficiently high (> 0.1 M) and (b) the equilibrium constant is fairly small. As a guideline, when determining the concentration of a buffer solution, use the Henderson–Hasselbalch equation if the [HA] or [Base] > 0.10 M and it is at least 103 times greater than the equilibrium constant.
If these requirements are not met, the equilibrium approach using an ICE table must be used. You can check the equilibrium approach for calculating the pH of buffer solutions and how it compares to the one using the Henderson–Hasselbalch equation here.
How is the Henderson–Hasselbalch Equation Derived?
It is derived from the expression for Ka by rearranging and taking the negative log of both sides of the equation:
HA(aq) + H2O(l ) ⇆ H3O+(aq) + A–(aq)
\[{K_{\rm{a}}}\; = \,\frac{{{\rm{[}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{][}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HA]}}}}\;\]
From this, we derive an expression for [H3O+]:
\[{\rm{[}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}\, = \,{K_{\rm{a}}}\;\frac{{{\rm{[HA]}}}}{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}\;\]
And now, taking a log of both sides, we get that:
\[{\rm{ – log}}\,{\rm{[}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}\,{\rm{ = }}\;{\rm{ – log}}\left( {{K_{\rm{a}}}\;\frac{{{\rm{[HA]}}}}{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}} \right)\]
\[{\rm{ – log}}\,{\rm{[}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}\,{\rm{ = }}\;{\rm{ – log}}\,{K_{\rm{a}}}\, – \,{\rm{log}}\,\frac{{{\rm{[HA]}}}}{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}\]
At this point, we can rearrange equation by changing the sign of the log and making [HA] as denominator:
\[{\rm{ – log}}\,{\rm{[}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}\,{\rm{ = }}\;{\rm{ – log}}\,{K_{\rm{a}}}\, + \,{\rm{log}}\,\frac{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HA]}}}}\]
Since pH = -log[H3O+] and pKa = -log Ka, the equation can be shown as:
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HA]}}}}\]
And this is the Henderson–Hasselbalch equation which is shown differently by changing the notation of the acid and its conjugate base:
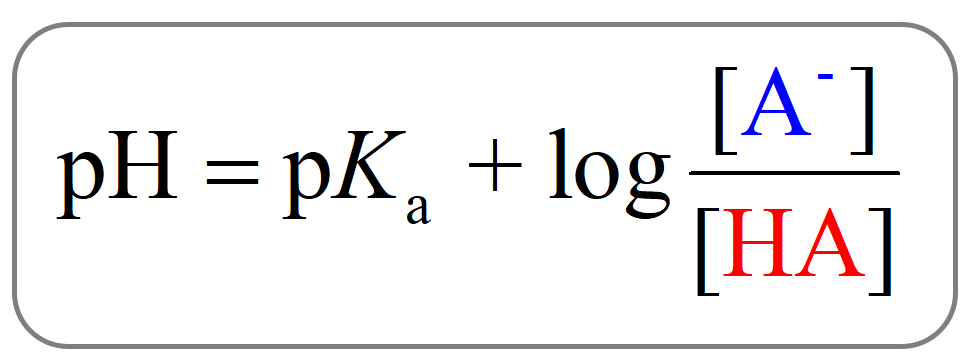
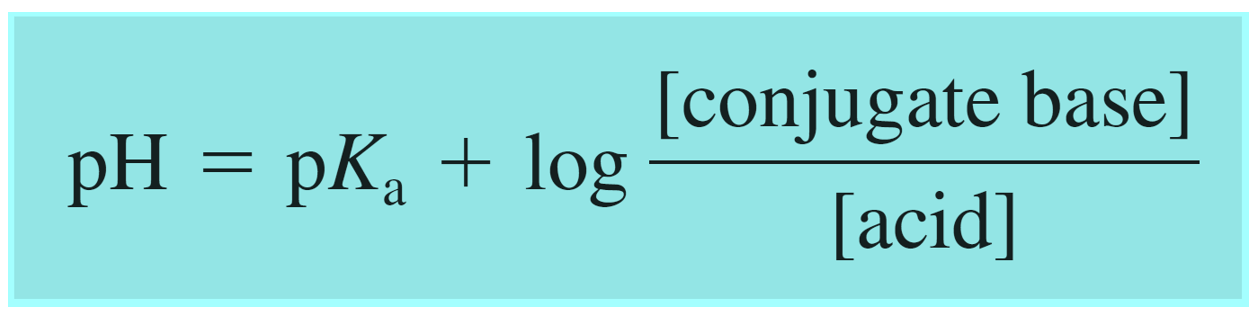
Buffers Containing a Base and Its Conjugate Acid
In the example above, we had a buffer composed of an acid and its conjugate base. However, remember, that a buffer can also be composed of a base and its conjugate acid which, unlike a regular acid, is an ion. Although this does not change the principle, you can write the Henderson–Hasselbalch equation using the words “base and acid”, instead of conjugate base and acid to avoid any confusion:
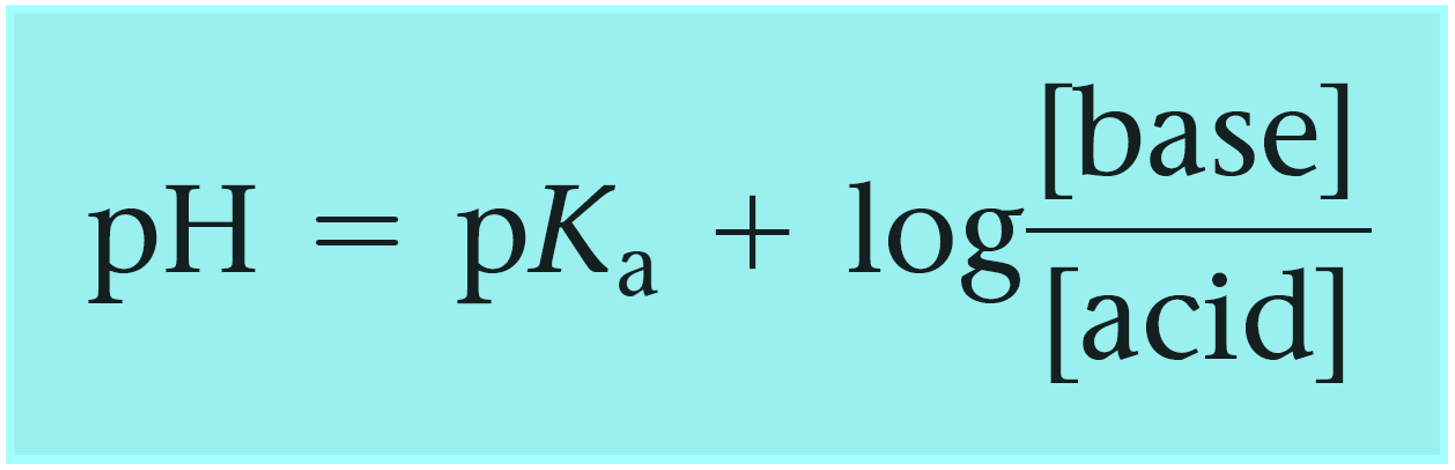
One common example of such buffer is the solution of weak base ammonia (NH3) and its conjugate acid ammonium chloride (NH4Cl).
The strategy for calculating the pH is similar to what we did before for the buffers containing a weak acid and its conjugate base.
The only extra step that you may need to do is to determine the pKa of the conjugate acid using its relationship to the pKb:
pKa + pKb = 14
For example,
Calculate the pH of a buffer solution containing 0.60 M in NH3 and 0.35 M in NH4Cl. The pKb of ammonia is 4.75.
The first step is to determine the pKa so that we can use it in the Henderson–Hasselbalch equation:
pKa + pKb = 14
pKa = 14 – pKb = 14 – 4.75 = 9.25
Because the concentrations of the buffer components are significantly higher than the Kb of ammonia, all we need to do, at this point, is plugging the numbers in the equation:
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HA]}}}}\]
\[{\rm{pH}}\; = \;9.25\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[0}}{\rm{.60]}}}}{{{\rm{[0}}{\rm{.35]}}}}\; = \;9.5\]
The Henderson–Hasselbalch equation gives some quick information and hints on choosing a proper buffer correlating pKa and the pH of the solution, and this is what we will discuss in the next couple of articles.
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- Preparing a Buffer with a Specific pH
- The Common Ion Effect
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of a Common Ion on Solubility
- The Effect of pH on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems

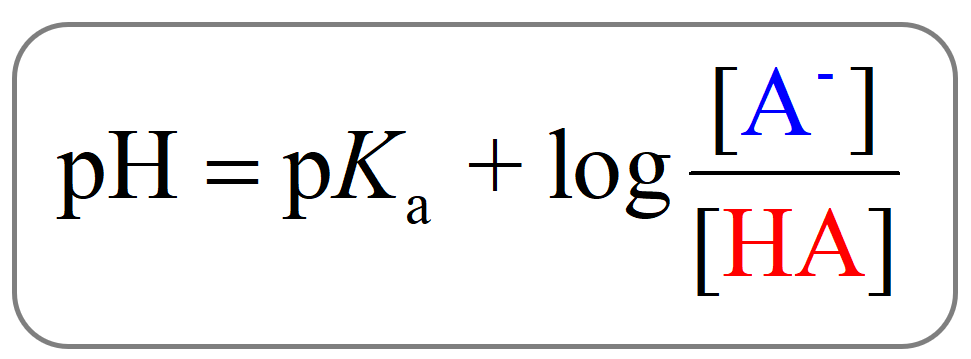
Hello, I think the numbers for 0.250 M and 0.400 M are switched 🙂
Thanks for letting me know! Fixed.