Significant figures are important in measurements and calculations, and you are going to see them quite often in chemistry. If you have already seen them, there is a chance that you feel slightly lost on getting the point of using them in every calculation. In this article, we will try to clear this confusion. So, first, what are the significant figures?

Let’s say you are using a ruler to measure the length of a calculator. Suppose the tip of the calculator stops between 13.4 and 13.5 cm:

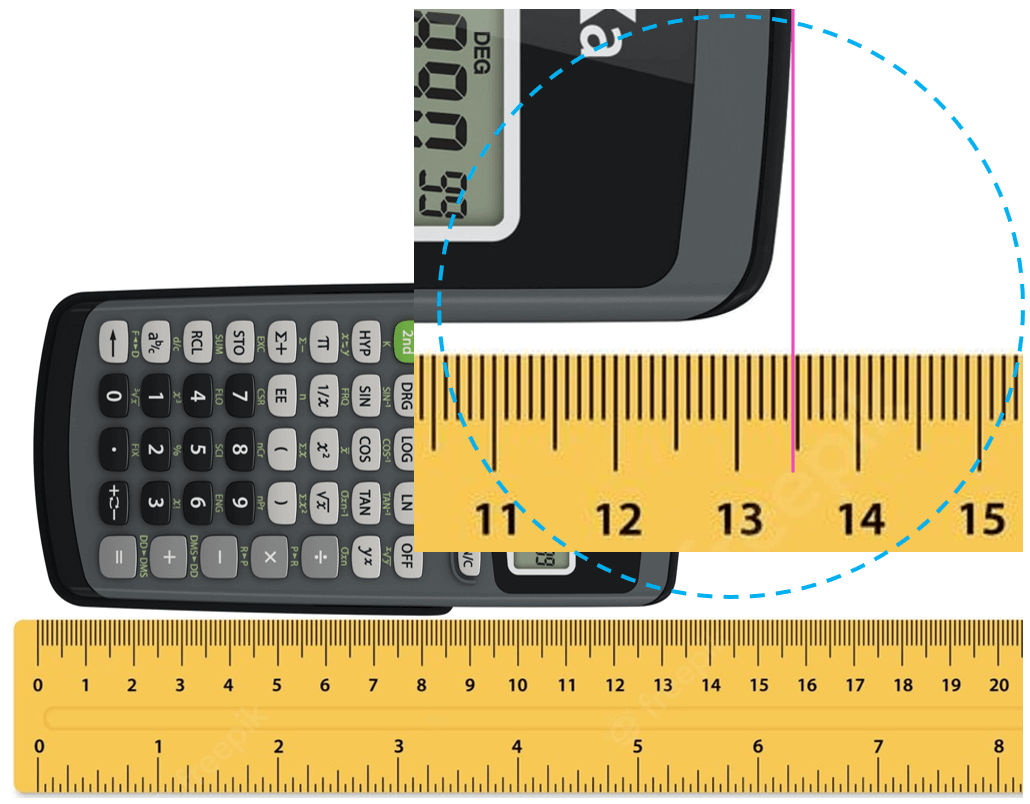
The question is how we know what the length is if the increment of the ruler is 0.1 cm (1 mm). Is it 13.48, 13.46, or maybe 13.45? And the answer is we cannot know this for sure because the precision of the measurement is limited by the ruler. What we do is estimate the last digit which can be for example by taking the average of 10 people who look at the reading of the ruler. The accepted approach here is to put all the numbers that are certain (in this case 13.4 – these are called certain digits), and one that is estimated (estimated number).

Let’s say we agree that it is 13.47 cm. All these numbers together, that is the certain digits and one estimated digit, make the significant figures of the measurement or simply significant numbers.

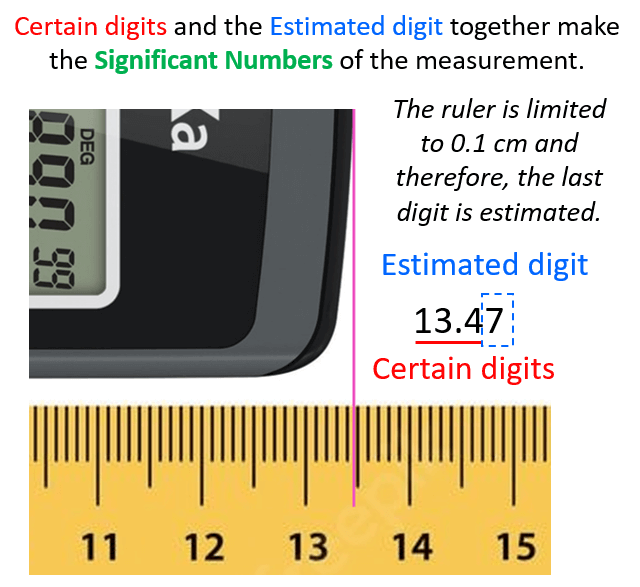
I emphasized the word measurement because, remember, significant figures are applicable for measurements. We will talk about this more, but now let’s see why the significant figures are important in calculation or should we say why the significant figures are significant.

Just like for measuring the length of the calculator, we are always limited by the accuracy of any measurement when mathematical operations are involved. For example, let’s say we measure the length of another calculator using a ruler with a 0.01 cm increment to be 15.628 cm, and we need to determine the length of the two calculators together.

Adding the numbers, we get 13.47 + 15.628 = 29.098 cm.

Notice that the answer is more precise than 13.47 because it has 3 decimal places which indicates more significant figures in this case. And this is not an accurate way of reporting the answer because we started with a number that only had 2 decimal places and we cannot have an answer that is more certain than any of the initial measurements. Therefore, there are rules that we must follow when doing mathematical operations in order to report the answer in a correct number of significant figures. So, remember, when doing calculations, we cannot suddenly have an answer that is more certain than the starting numbers because the calculation is based on those initial measurements. Before going over the rules for mathematical operations, let’s first address an important question:

How do I Identify the Significant Figures in a Number?

The first rule is simple, any nonzero number is a significant figure. For example, 26 has two S.F., 164 has three S.F., 18948 has five S.F. and etc.

It is the zeros that can be either significant or nonsignificant depending on where in the number they are located. First, let’s address the ones that are in between nonzero numbers. These are called interior zeroes and are considered significant figures. For example, 6204 has 4 S.F., 84069 has 5 S.F., and 204 has 3 S.F.

If the zeros are at the end of the number (trailing zeroes), they are considered nonsignificant, unless there is a decimal place!

For example, the zero in 250 is a nonsignificant number, while the one in 25.0 is significant. The reason for this is that in 250, the zero does not add any certainty to the measurement and only increases the number 25 by an order of ten. Remember, significant figures are about the certainty of the measurement and not just any digit that appears in the number. Just because the number is larger, it does not mean it has more significant figures. 8000 has only one significant figure but 8.0 has two significant figures. So, the zeros after the decimal place are important in that they tell us about the certainty of the measurement while in the absence of a decimal place, they only tell us about the magnitude of the number which has nothing to do with the certainty of the measurement.

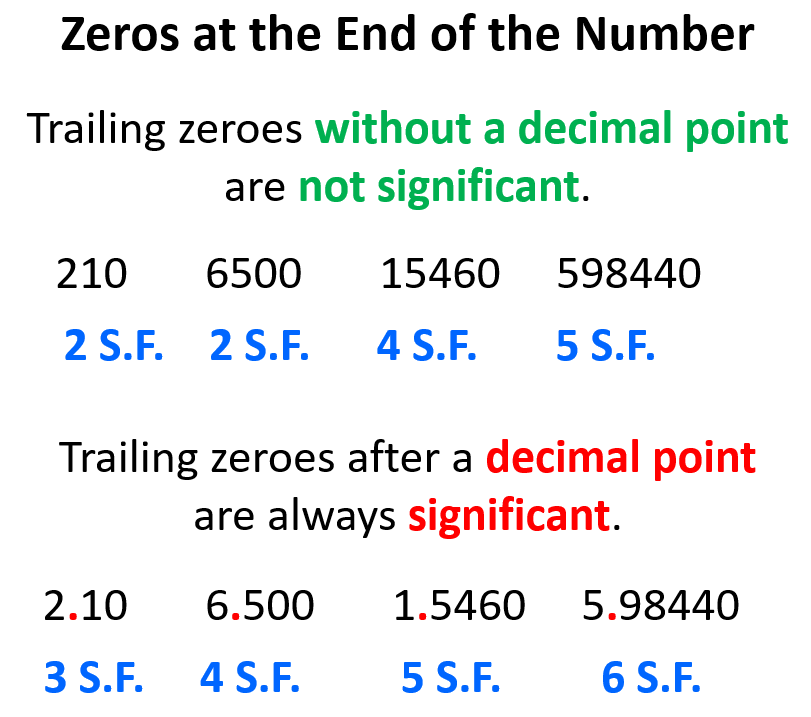
If the trailing zero appears before the decimal point with following zeroes, then this zero is also a significant number:

The same goes for zeros that stand before the first nonzero digit (leading zeroes). These again only tell us how small the number is and not how accurate the measurement was.

For example, the number 75 is as certain as 0.75. They both have two significant figures, and one is 100 times smaller than the other, but that is it as the zero does not make the measurement any certain. On the other hand, if we have 0.750, we should realize that the last zero adds certainly to the measurement and therefore, it is a significant figure, and the number has three significant figures.

Notice that the zero between 5 and 8 is significant, and so is the one at the end of the last number because there is a decimal place. In any case, the zeros before the first nonzero digit are not significant.

Significant Figures and Scientific Notation

We often work with extremely large or small numbers in chemistry which can be written or understood wrongly if one zero is misplaced. To avoid these mistakes and represented the numbers easier, the scientific notation is used which has a general form of N × 10ⁿ

N here is a number between 1 and 10 and n is the exponent that can be a positive or negative integer (whole number).

For example, 1.34 x 10⁵ = 134,000, 8.6 x 10^-4 = 0.00086.

For counting the number of significant figures in scientific notation, we focus on the N, that is the number that comes before the 10ⁿ. The exponent is only to tell us about the magnitude of the number.

Therefore, 1.34 x 10⁵ has 3 significant figures, and 8.6 x 10^-4 has 2 significant figures. 1.34 x 10⁵ written as 134,000 has 6 digits and if we wanted to express 1.34 x 10⁵ with 6 significant figures, we need to add the zeros after the decimal point in the initial number: 1.34000 x 10⁵.

On the other hand, if the number has more digits than it is supposed to have, the initial number is rounded off according to how many significant figures there should be. For example, how can we express 46897 in two significant figures?

What we do in this case is round up the 6 to seven as there is an 8 after it, and add the corresponding exponent: 4.7 x 10⁴.

Exact Numbers

These are the numbers that do not have any uncertainty and therefore, they do not limit the number of significant figures.

For example, there are five fingers on a hand, and that number is an exact number. It is not like we can argue that it is 5.01 or 5.0056 depending on how we look at it. In other words, we do not use an instrument with certain precision to measure this number. Therefore, these are called exact numbers and they have an infinite number of significant figures. Another example can be when we say that one inch is equal to 2.54 cm. When doing calculations involving this correlation, we do not limit the number of significant figures by 3 because, 2.54 has an infinite number of significant figures and we can say, for example, that 1 in = 2.540000 cm. Same, 5 atoms means 5.0000… atoms, and 8 vehicles mean 8.0000… vehicles.

This is important when doing calculations, as you need to remember that the number of significant figures in the answer is dictated by the other number and not the one given with exact numbers. We will discuss the significant figures and mathematical operations in the next article as this has been quite a lot of information already.

Check Also

• Significant Figures in Addition, Subtraction Multiplication, and Division
• Significant Figures Practice Problems
• Converting Units With Conversion Factors Dimensional Analysis
• Conversion Factors and Dimensional Analysis Practice Problems
• Density Practice Problems