General Chemistry

Ksp – The Solubility Product Constant

Remember, earlier when discussing precipitation reactions, we used tables with rules for solubility to classify compounds as water-soluble or insoluble. For example, BaCl2, according to the rules, is soluble, while BaSO4 is insoluble in water. However, these definitions are not to understand as black and white. All the compounds are soluble in water or any other solvent, and the question is to what extent they are. To quantify how much a given compound dissolves in water, we use the equilibrium constant for its dissociation reaction.

For example, BaSO4 dissociates into Ba2+ and SO42- ions, and because the salt is solid, this equation represents its dissolution:

 

BaSO4(s) ⇆ Ba2+(aq) + SO42-(aq)

 

The equilibrium constant representing the dissolution of an ionic compound is called the solubility product constant (Ksp) where sp stands for solubility product. For BaSO4, the expression of the solubility product would be:

 

Ksp = [Ba2+][ SO42-]

 

Remember, for a general reaction, the equilibrium constant includes the stoichiometric coefficients and is given by the following equation:

 

 

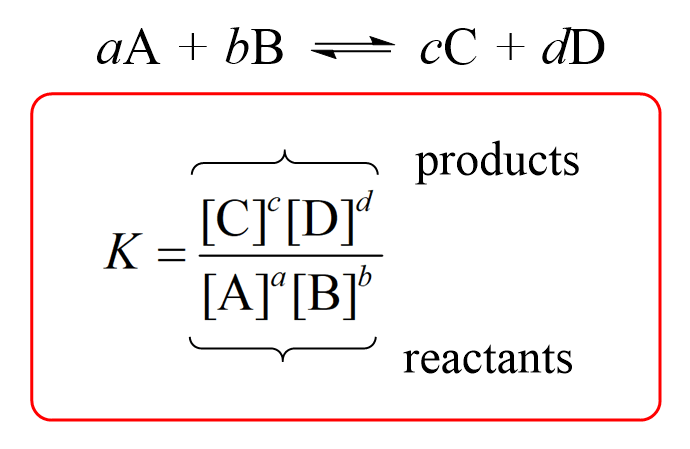
Therefore, the Ksp for CaF2 and Ag3(PO4) would be:

 

CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)

Ksp = [Ca2+][F–]2

 

 Ag3(PO4) (s) ⇆ 3Ag+(aq) + PO43-(aq)

Ksp = [Ag+]3[PO43-]

 

Notice that in all Ksp expressions, the salt was missing, and the reason for this is that, remember, solids do not appear in the equilibrium constant expressions for heterogeneous equilibrium.

The magnitude of Ksp is a measure of the solubility of a compound – the larger the value, the more soluble the compound is in water. However, we cannot compare the Ksp values of any two compounds to tell which is more soluble because of the concentrations raised to the power of coefficients. Therefore, use the Ksp values to compare the solubilities of compounds with the same cation-anion ratio such as AgBr and CdS, or CaF2 and PbCl2.If the Ksp values vary in orders of magnitude, then, of course, we can pick the more soluble compounds.

The values of Ksp at 25 °C for many ionic solids can be found in an Appendix of a general chemistry textbook.

 

Calculating Ksp from Concentrations

One thing to keep in mind in calculations regarding Ksp and solubility is that they apply to saturated solutions because if we add for example, 1 g of a salt to gallon of water, the resulting concentrations may change if we add some more of the salt. The final and correct values of the concentrations are only achieved when the solution is saturated.

Example,

Calculate Ksp for silver chromate if the concentration of silver ions in its saturated solution is 1.3 x 10-4 M.

First, write the dissociation equation of silver chromate:

Ag2(CrO4) (s) ⇆ 2Ag+(aq) + CrO42-(aq)

Next, write the expression for the solubility product:

Ksp = [Ag+]2[ CrO42-]

Now, the concentration of chromate ions is going to be twice smaller because, for every 2 moles of Ag+, there is one mole of CrO42- formed.

We can calculate this by the mole ratio method too:

\[M\,{\rm{(Cr}}{{\rm{O}}_{\rm{4}}}^{{\rm{2 – }}}{\rm{)}}\;{\rm{ = }}\,{\rm{1}}{\rm{.3}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 4}}}}\,\frac{{\cancel{{{\rm{mol}}\,{\rm{A}}{{\rm{g}}^{\rm{ + }}}}}}}{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}\,{\rm{Cr}}{{\rm{O}}_{\rm{4}}}^{{\rm{2 – }}}\,}}{{{\rm{2}}\,\cancel{{{\rm{mol}}\,{\rm{A}}{{\rm{g}}^{\rm{ + }}}}}}}\; = \,6.5\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 5}}}}\,{\rm{mol/L}}\]

Therefore, the Ksp is:

Ksp = [Ag+]2[ CrO42-] = (1.3 x 10-4)2 x 6.5 x 10-5 =  1.1 x 10-12

 

Molar Solubility

The terms molar solubility and solubility product may be confusing as they are similar but not the same. The solubility product is the Ksp which is the product of the ions raised to their coefficients.

For example, when we say the solubility product (Ksp) of CaF2 is 3.9 x 10-11, it means that;

 

Ksp = [Ca2+][ F–]2 = 3.9 x 10-11

 

The molar solubility is the solubility in units of moles per liter (mol/L). Sometimes, the solubility is also given in grams per liter. Now, the molar solubility of CaF2 can be calculated from the Ksp value by setting up an equation with an unknown. For this, we need the dissociation equation first:

 

CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)

 

If we assume that x mol/L of CaF2 is dissolved in a saturated solution, the concentration of the Ca2+ and F– ions would be x mol/L and 2x mol/L respectively. This is based on their mole ratio of the chemical equation.

You can also set up an ICE table to determine these values:

 

x           x                2x    
CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)

  [Ca2+] [F–]
Initial 0 0
Change +x +2x
Equil x 2x

 

So, the expression for Ksp can be written as:

 

Ksp = [Ca2+][ F–]2 = (x)(2x)2 = 3.9 x 10-11

 

Therefore,

(x)(2x)2 = 3.9 x 10-11

4x3 = 3.9 x 10-11

 x = 2.1 x 10-4

 

Now, 2.1 x 10-4 mol/L is the concentration of dissolved CaF2 because it is in 1:1 ratio with Ca2+, and this is the molar solubility of CaF2. So, in any (almost) saturated solution of CaF2 at 25 oC, regardless of its volume the concentration of CaF2 is 2.1 x 10-4 mol/L. There are factors such as the temperature, pH, and presence of other ions in the solution that affect the solubility, and we will discuss them in the next few articles.

 

Calculating Ksp from Solubility

We can also calculate the Ksp from the molar solubility of the salt.

For example,

Calculate the Ksp value for bismuth sulfide (Bi2S3) if its solubility is 1.0 x 10-15  mol/L at 25 oC.

First, write the dissociation equation of Bi2S3:

 

Bi2S3(s) ⇆ 2Bi3+(aq) + 3S2-(aq)

 

The solubility product constant is:

 

Ksp = [Bi3+]2[S2-]3

 

The solubility value tells us how much of the salt dissociates to ions, so this is the concentration of the salt in the equation. Therefore, we can calculate the concentration of the ions based on their molar ratio with the salt.

 

\[M\,{\rm{(B}}{{\rm{i}}^{{\rm{3 + }}}}{\rm{)}}\;{\rm{ = }}\,{\rm{1}}{\rm{.0}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 15}}}}\,\frac{{\cancel{{{\rm{mol}}\,{\rm{B}}{{\rm{i}}_{\rm{2}}}{{\rm{S}}_{\rm{3}}}}}}}{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{2}}\,{\rm{mol}}\,{\rm{B}}{{\rm{i}}^{{\rm{3 + }}}}\,}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{B}}{{\rm{i}}_{\rm{2}}}{{\rm{S}}_{\rm{3}}}}}}}\;{\rm{ = }}\,{\rm{2}}{\rm{.0}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 15}}}}\,{\rm{mol/L}}\]

 

\[M\,{\rm{(}}{{\rm{S}}^{{\rm{2 – }}}}{\rm{)}}\;{\rm{ = }}\,{\rm{1}}{\rm{.0}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 15}}}}\,\frac{{\cancel{{{\rm{mol}}\,{\rm{B}}{{\rm{i}}_{\rm{2}}}{{\rm{S}}_{\rm{3}}}}}}}{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{3}}\,{\rm{mol}}\,{{\rm{S}}^{{\rm{2 – }}}}\,}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{B}}{{\rm{i}}_{\rm{2}}}{{\rm{S}}_{\rm{3}}}}}}}\;{\rm{ = }}\,{\rm{3}}{\rm{.0}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 15}}}}\,{\rm{mol/L}}\]

 

Therefore,

Ksp = [Bi3+]2[S2-]3 = (2.0 x 10-15)2 (3.0 x 10-15)3 = 1.1 x 10-73

 

Check Also

Leave a Comment