In first-order reactions, the rate of the reaction is directly/linearly proportional to the concentration of the reactant. This can be seen in the differential rate law which shows how the rate of a reaction depends on the concentration of the reactant(s):
A → Products
Rate = k[A]1
where k is the rate constant, and the exponent 1 is the reaction order, which, in a general formula, is given by n.
Now, when n = 1, we have a first-order reaction where the rate changes linearly with the concentration of A. For example, let’s say the concentration of A changes from 3 M to 6 M. The rate for these two concentrations would be:
Rate1 = k[3]1 = 3k
Rate2 = k[6]1 = 6k
The rate increases two times when we double the concertation of A. So, remember, in first-order reactions, the rate is directly proportional to the concentration of the reactant that appears in the rate law.
The Units of Rate Constant, k for a First-Order Reaction
Most often, the reaction rate shows how the concentration changes with time, and therefore, the units of the rate are mol/L. If we rearrange the equation, we can obtain an expression for the rate constant as follows:
\[k\; = \;\frac{{{\rm{rate}}}}{{\left[ {\rm{A}} \right]}}\]
And now, we can add the units for the rate and concentration and see what we obtain for the rate constant:
\[k\; = \;\frac{{{\rm{mol}}}}{{{\rm{L}}\; \times \;{\rm{s}}}}\; \div \;\frac{{{\rm{mol}}}}{{{\rm{L}}\;}}\; = \;\frac{{\cancel{{{\rm{mol}}}}}}{{\cancel{{\rm{L}}}\; \times \;{\rm{s}}}}\; \times \;\frac{{\cancel{{\rm{L}}}}}{{\cancel{{{\rm{mol}}}}}}\; = \;{{\rm{s}}^{{\rm{ – 1}}}}\]
There is also a formula which you can use as a shortcut to determine the units of a rate constant:
k units = M1-n · t-1
where n is the reaction order
If we needed to determine the units of k for a first-order reaction, we would use 1 for the n:
k units = M1-1 · t-1 = t-1
So, if the time is given in seconds, k would be s-1, for minutes, min-1, and so forth.
Another example, let’s say we want to determine the units of the rate constant for third-order reactions.
n = 3, and therefore,
k units = M1-3 · t-1 = M-2 · t-1
If the time is seconds, then the units will be:
k units = M-2 · s-1
The Integrated Rate Law of a First-Order Reaction
Integrating the differential rate law, we obtain the integrated rate law for the first-order reactions. You can check this article for more details, but for now, we will write the final form of the integrated rate law for first-order reactions:
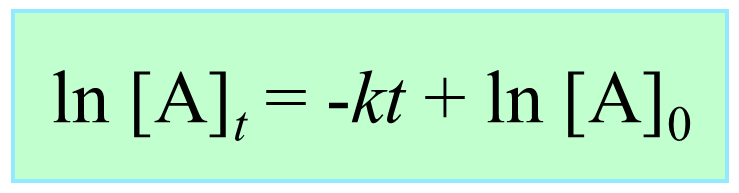
What is important here is to notice that the integrated rate law for first-order reactions has the form of an equation for a straight line and plotting ln [A]t versus time yields a straight line with a slope of –k and a y-intercept of ln [A]0.

If we plot the concentration instead of its logarithm, an exponential decrease will be obtained rather than a straight line. And this is an important strategy for determining the order of a reaction because the straight line of each order is obtained with the plot of different data such as the concentration, the log, or the reciprocal of it. This also is covered in a separate article, so be sure to check it out as determining the reaction order is a very common type of question in kinetics.
The integrated rate law is often given the following form where the concentrations are combined in the logarithm:
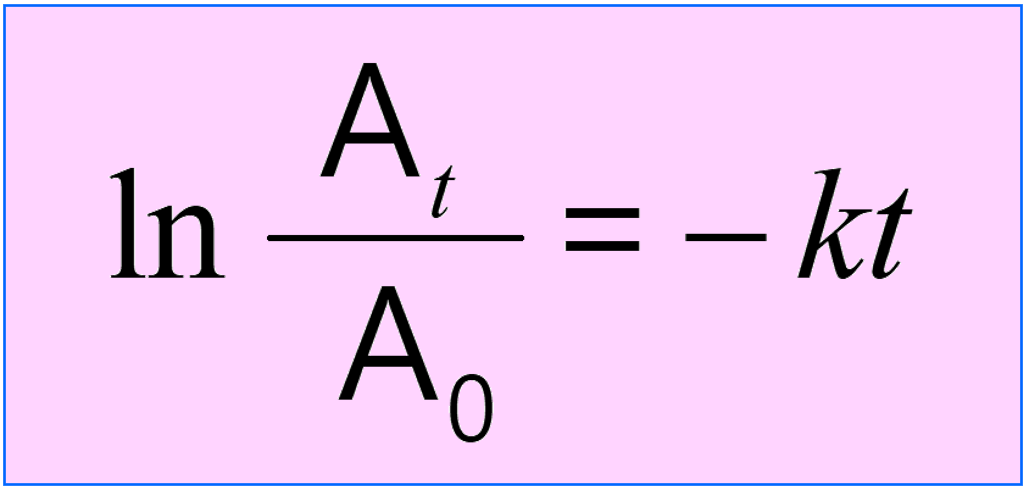
The Applications of the Integrated Rate Laws?
So, we have obtained the equation and the graph for the integrated rate laws, and the question is what do we use them for?
There are two main applications, at least two main types of problems, you will be given in your class based on the integrated rate laws:
- One is determining the concentration of a reactant or product at a certain point of the reaction when the reaction order is provided.
- The second is actually determining the rate law based on the data on how the concentration changes with time.
Let’s do an example of determining the concertation of a reactant when the reaction order is given.
Example:
Dinitrogen pentoxide, N2O5, decomposes by a first-order reaction according to the following equation:
2N2O5(g) → 2N2O4(g) + O2(g) k = 3.4 x 10-6/s
What would be the concentration of N2O5 after running the reaction for 3.00 hr if the initial concentration of N2O5 was 0.0465 mol/L?
Solution:
The integrated rate law for first-order reactions can be written as:
ln [A]t = –kt + ln [A]0
Let [N2O5]0 be 0.0465 M, and [N2O5]t be the concentration after 3.00 hr. Because the rate constant is expressed using seconds, 3.00 hr must be converted to seconds, which is 3.00 x 3600 s = 10800 s. Substituting these and k = 3.4 x 10-6/s into the first-order rate equation gives:
\[{\rm{ln [}}{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{5}}}{{\rm{]}}_t}\; = {\rm{ }} – 3.4{\rm{ }} \times {\rm{ }}{10^{ – 6}}\,\cancel{{{s^{ – 1}}}}\, \times \,10800\,\cancel{s}\; + \;\ln \,(0.0465)\,\]
ln [N2O5]t = -0.03672 – 3.07
ln [N2O5]t = -3.105
[N2O5]t = e-3.105 = 0.0448 M
The Half-Life of First-Order Reactions
The half-life (t1/2) of a reaction is the time required for the concentration of a reactant to drop to one-half of its initial value. It depends on the order of the reaction, and it is obtained from the corresponding integrated rate law.
The half-life of the first-order reactions is obtained from the integrated rate law by replacing [A]t with 1/2[A]0:
\[\ln \;\frac{{{{[A]}_t}}}{{ {{[A]}_0}}}\; = \; – kt\]
Half-life is when the initial concentration [A]0 dropped by 50% which means
\[\ln \;\frac{{{\textstyle{1 \over 2}}\cancel{{{{[A]}_0}}}}}{{ \cancel{{{{[A]}_0}}}}}\; = \;\ln \frac{1}{2}\, = \; – k{t_{1/2}}\]
Therefore,
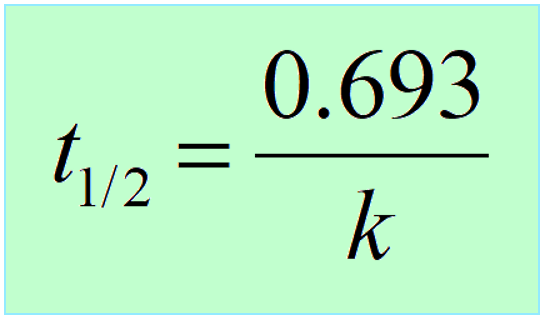
Interestingly, the half-life of first-order reactions does not depend on the initial concentration of the reactant.
So, if we start a reaction with a 10 M reactant, it will take the same time for it to decrease to 5 M as it does for dropping from 5 M to 2.5 M, and consequently from 2.5 M to 1.25 M.
The reason for this is that in a first-order reaction, the reactant molecules do not collide with proper energy and orientation which is the requirement for a reaction between two molecules to occur. Each molecule transforms into the product(s) by itself and has no effect on the reaction rate. Perhaps, the example of a cable car is a good analogy: if it takes 10 min to reach the destination, the number of people (reactant concentration) in the cabin does not matter.
Below is a summary of the correlation between the half-life and concentration of reactants for a first-, second-, and zero-order reactions:
How to Determine the Concentration from Half-life
Notice that the independence of half-life from the concentration of reactant(s) is unique to first-order reactions, which allows us to more easily predict how much the concentration of the reactant will drop in a given time.
For example, let’s say we need to determine the concentration of 0.64 M A after 56 hours given its half-life is 14 hours and the reaction follows first-order.
A → B
It is always a good idea to compare the time of the reaction given in the problem, to the half-life of the reaction. Now, it may not be evident how many half-lives the given time takes, and therefore, it is always a good idea to divide the time of the decay, given in the problem, by the half-life of the reaction. If we divide the time (56 hours) by the half-life (14 hours), we will find out that the process takes 4 half-lives:
56 : 14 = 4
This means the concentration of the reactant is going to be halved 4 times:
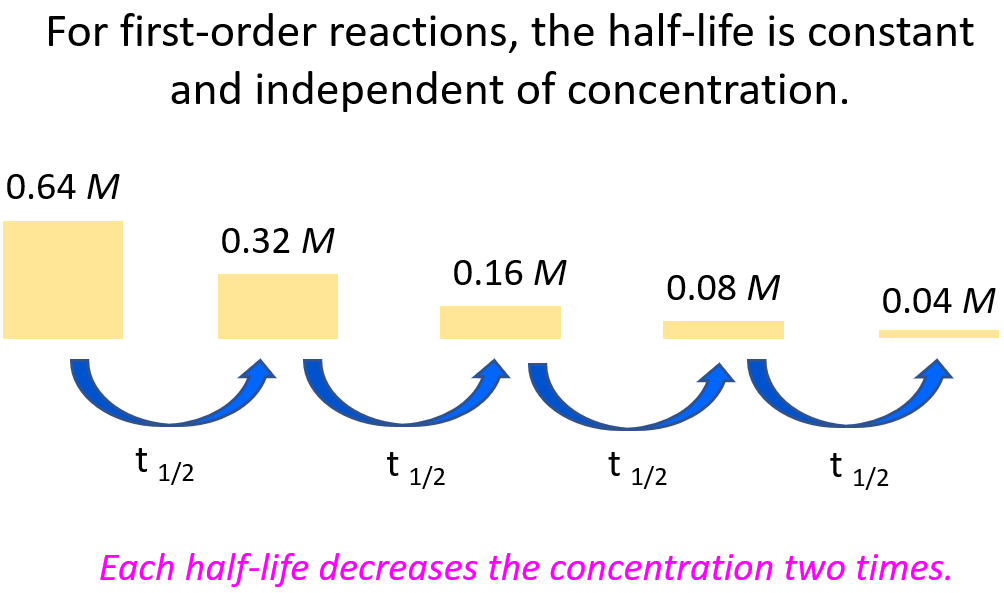
Once you understand this concept, you do not have to draw the half-life segments, especially if the ratio of the time and the half-life is not a whole number. Instead, you can use the following formula to calculate the remaining concentration after the given time:

The exponent indicates how many times the initial amount is halved. For example, if it was one time, we would simply multiply the initial amount by ½, if it is two times, then we multiply by ½ two times, and so forth.
Therefore, in this case, the exponent is 4 because the time corresponds to 4 half-lives.
\[{\rm{[A]}}\,{\rm{ = }}\,{{\rm{[A]}}_{0\;}} \times \,{\left( {\frac{1}{2}} \right)^4}\]
\[{\rm{[A]}}\,{\rm{ = }}\,0.64 \times \,{\left( {\frac{1}{2}} \right)^4}\; = \;0.080\,M\]
A little exercise for you – try to solve this problem by using the integrated rate law of first-order reactions.
Exercise 2: Use the shortcut formula to confirm the answer to the problem we discussed earlier:
Dinitrogen pentoxide, N2O5, decomposes by a first-order reaction according to the following equation:
2N2O5(g) → 2N2O4(g) + O2(g) k = 3.4 x 10-6/s
What would be the concentration of N2O5 after running the reaction for 3.00 hr if the initial concentration of N2O5 was 0.0465 mol/L?
First-order reactions are in general of the greatest importance as they are characteristic of nuclear reactions which have many applications such as nuclear power stations, nuclear weapons, and carbon dating for determining the age of ancient objects.
We have a good collection of practice problems on the kinetics of nuclear reactions which you can find here.
Check Also
- Reaction Rate
- Rate Law and Reaction Order
- How to Determine the Reaction Order
- Integrated Rate Law
- The Half-Life of a Reaction
- Determining the Reaction Order Using Graphs
- Units of Rate Constant k
- How Are Integrated Rate Laws Obtained
- Activation Energy
- The Arrhenius Equation
- Chemical Kinetics Practice Problems
- Carbon Dating Practice Problems
- Half-Life and Radioactivity Practice Problems

