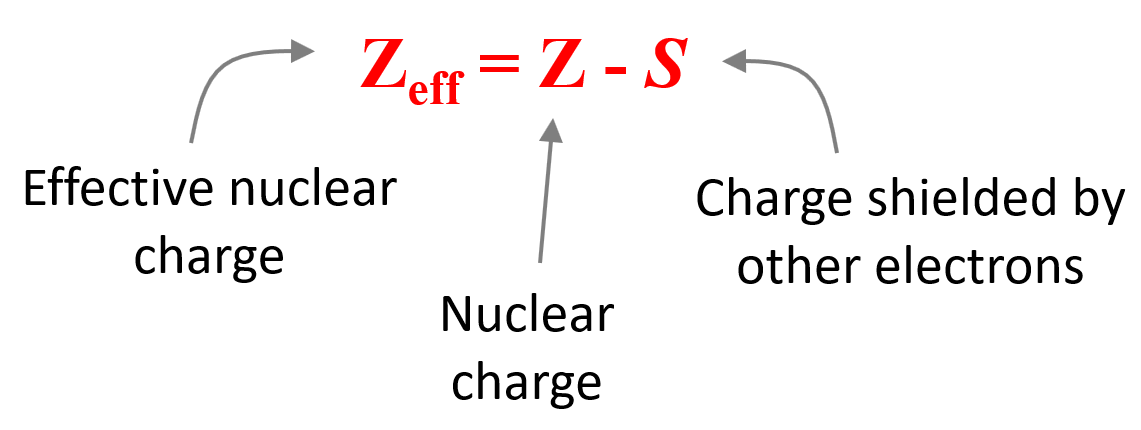
Periodic Properties and Periodic Trends

Effective Nuclear Charge

Effective nuclear charge (Z_eff) is the nuclear charge an electron actually experiences. Let’s understand what this statement means.

We know from basic physics that opposite electrical charges attract, and if we consider the hydrogen atom, it is fairly straightforward to understand that there is an attractive force between the positively charged nucleus and the negatively charged electron. The electron experiences the 1+ charge of the nucleus:

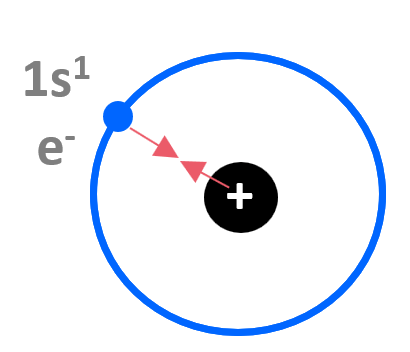
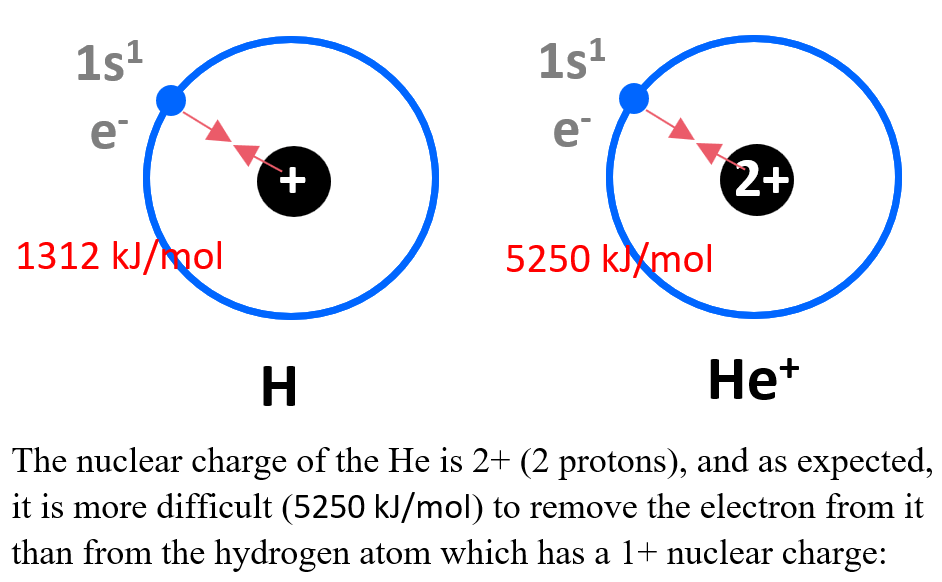
It takes 1312 kJ/mol of energy to remove the 1s electron from hydrogen.

Let’s compare this to the energy required to remove the 1s electron from He⁺ ion. How do you think the energies compare?

According to Coulomb’s law, the strength of this interaction depends on the magnitudes of the charges and the distance between them. The nuclear charge of the He is 2+ (2 protons), and as expected, it is more difficult (5250 kJ/mol) to remove the electron from it than from the hydrogen atom which has a 1+ nuclear charge:

Shielding by Electrons

The comparison of the nuclear charge experienced by the electron in the hydrogen atom and the He⁺ion illustrates how increasing the magnitude of the opposite charge increases the attraction forces between the particles. Now, aside from the attractive forces, there are also repulsive forces that occur between particles with the same charge. So, if there is another electron(s) between the one we study and the nucleus, the attractive forces must decrease because of the shielding/screening effect of the electron that is in between the nucleus and the electron being studied.

Shielding by Electrons in Inner Energy Levels

For example, the nuclear charge of Li is 3+, but that is not what the electron in the outermost energy level (valence shell) experiences. Recall that we classify electrons as valence (those in the outermost energy level), and core electrons. The electron configuration of Li is 1s²2s¹, and the 1s valence electron does not experience the 3+ charge of the nucleus because of the shielding by the two core electrons (2s²):

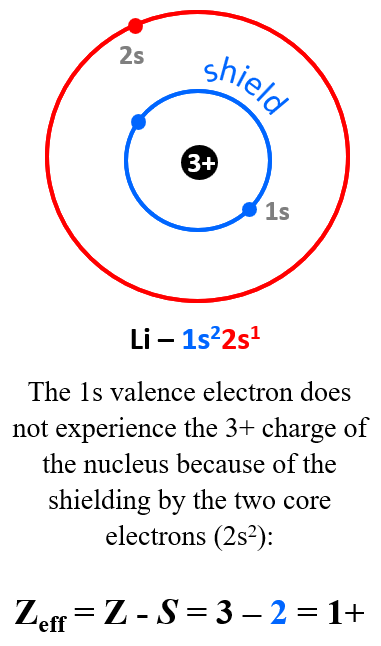
The effective nuclear charge of Li (that is what the valence electron experiences) is the difference between the nuclear charge and the number of core electrons:

So, for Li, it would be:

Z_eff = Z – S = 3 – 2 = 1+

Now, because the nuclear charge is equal to the atomic number, and the screening electrons are those in the core level, we can also write this formula as:

Z_eff = Atomic number – # core electrons

Let’s use this formula to calculate the effective nuclear charge of fluorine. The electron configuration of fluorine is 1s²2s²2p⁵, so it has seven valence electrons and two core electrons. The effective nuclear charge experienced by any of the valence electrons is 9 – 2 = 7+.

This is the simple method for determining the effective nuclear charge because we do not consider the shielding effect of the electrons in the same energy level, and for those we consider, we take the effect equal for all the electrons. In the next sections, we will discuss these factors as well.

Effective Nuclear Charge and Periodic Table

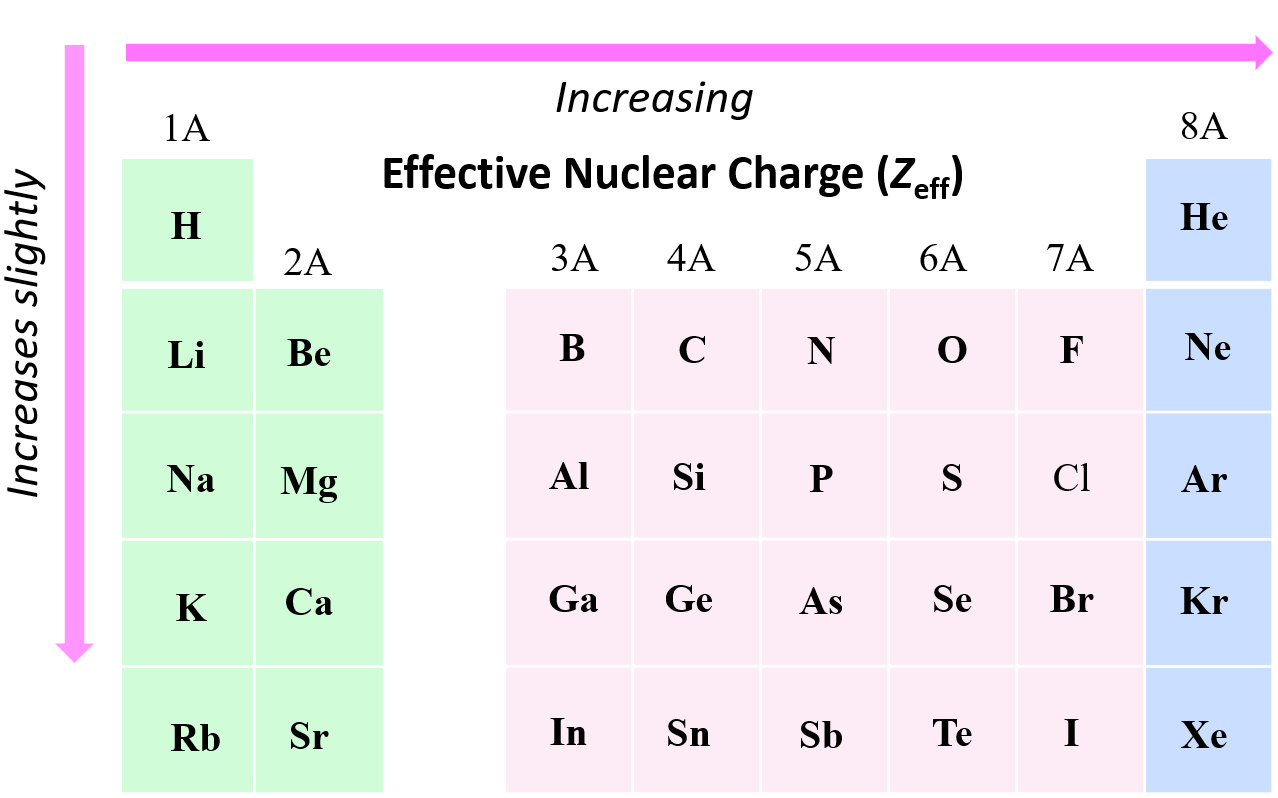
We have seen that the effective nuclear charge of fluorine is significantly greater than that of hydrogen or lithium, and this is a general trend that Z_eff increases from left to right across a row in the periodic table. In general, as the effective nuclear charge increases, the atomic radius gets smaller.

The reason for this is, as we move to the right, the nuclear charge increases while the number of core electrons stays constant, and as a result, the valence electrons experience a stronger attraction force with the nucleus. Yes, the number of valence electrons increases as well, but these have a significantly lower shielding effect, and each of them experiences a greater effective nuclear charge. For example, let’s compare the effective nuclear charges of Li and fluorine:

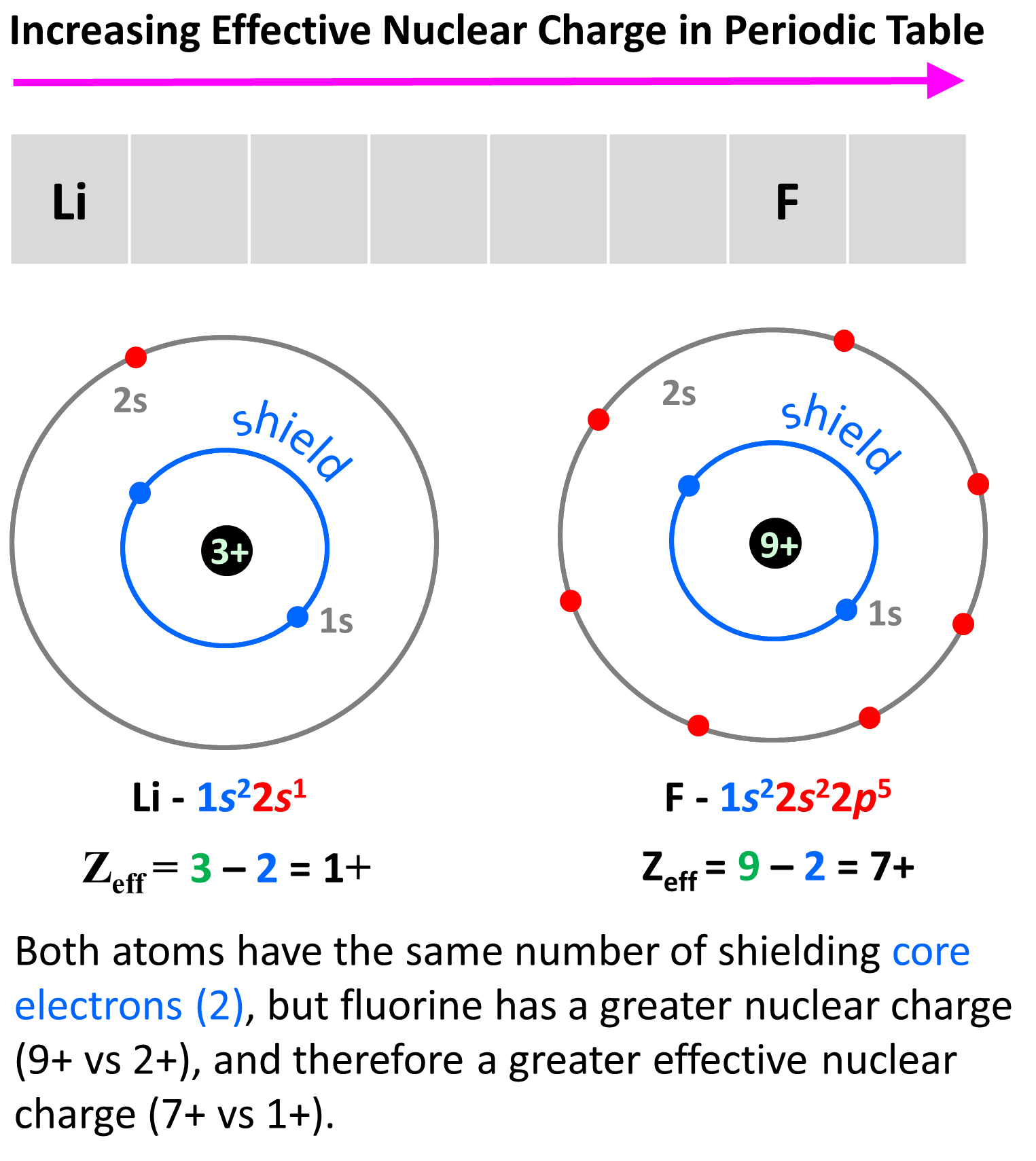
Li has a nuclear charge of 1+ and two core electrons, while fluorine also has two core electrons, but its nuclear charge is 9+. The effective charges are, therefore, 3 – 2 = 1+, and 9 – 2 = 7+ respectively.

The effective nuclear charge does not change much within a group because the number of core electrons increases with the nuclear charge. For example, the effective nuclear charge of sodium and lithium is the same using the simple method:

Z_eff (Li) = 3 – 2 = 1+

Z_eff (Na) = 11 -10 = 1+

However, there is a slight increase in effective nuclear charge moving down a group. The reason for this is the increasing size of the atomic orbitals which makes the core electron cloud more diffuse, thus providing less shielding of the nuclear charge experienced by the valence electrons.

Shielding by Other Electrons in the Same Energy Level

In the lithium atom, there is only one valence electron, and the shielding was caused only by the core electrons which are closer to the nucleus. In many atoms, however, there is more than one electron in the valence shell, so do they affect the nuclear charge of their fellow electrons in the same level? The short answer is yes, they do, but very often we ignore it because it is very small compared to the shielding effect of the core electrons.

For example, the electron configuration of beryllium is 1s²2s², and despite the 4+ nuclear charge, the effective nuclear charge experienced by Be’s outermost electrons is approximately 2+ because of the shielding by the two 1s core electrons:

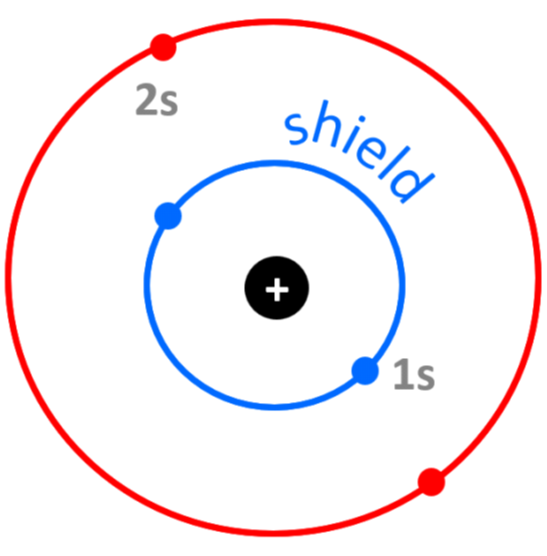
Z_eff = Z – S = 4 – 2 = 2+

Slater’s Rule to Calculate The Effective Nuclear Charge

The more accurate way of calculating the effective nuclear charge is Slater’s Rule which differentiates the effect of each electron depending on its energy level. Each electron gets a coefficient in the formula for the effective nuclear charge which, fr the main group elements, is as follows:

The electrons farther away from the valence electrons, meaning the ones closest to the nucleus, have the greatest shielding effect, and they get a coefficient of 1. The electrons one energy level below have a coefficient of 0.85, and those in the same energy level have only a 0.35 coefficient.

So, for Be (1s²2s²), we have one electron in the same (n) level because we do not count the electron we are studying, and we have two electrons in the n-1 level. The coefficients are then 0.35 and 0.85 respectively and the effective nuclear charge will be Z_eff= Z – S = 4 – (0.35 x 1) + (0.85 x 2) = 1.95+

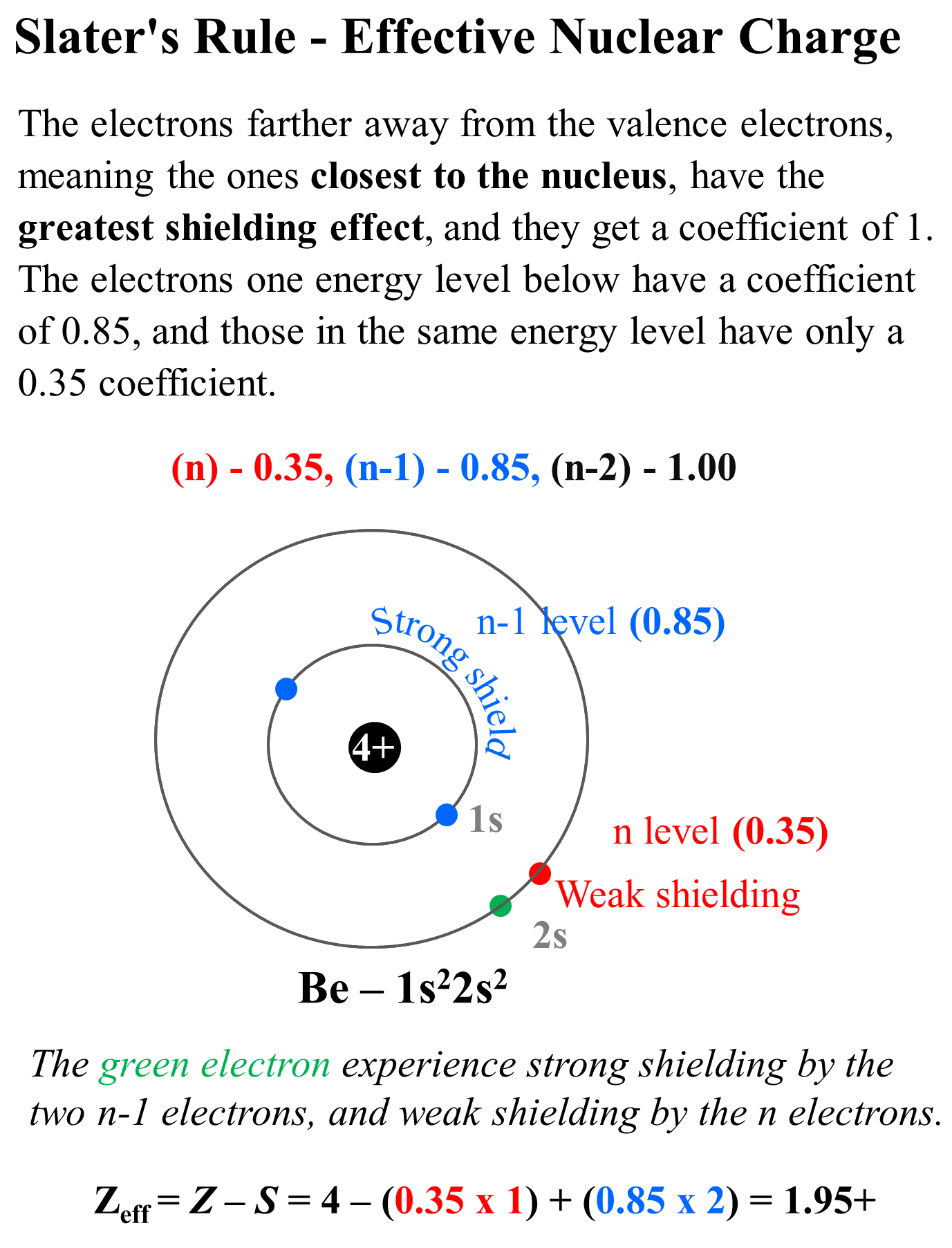
So, the effective nuclear charge is slightly smaller because we consider the effect of valence electrons.

Let’s also compare the effective nuclear charge of fluorine determined by the simple method and Slater’s method. The electron configuration of fluorine is 1s²2s²2p⁵, so to calculate the effective nuclear charge, we need to consider that it has six electrons in the n level and two electrons in the n-1 level. The effective nuclear charge experienced by any of the valence electrons would then be:

Z_eff= Z – S = 9 – (0.35 x 6) + (0.85 x 2) = 5.2+

And again, it is a little lower than the simple estimate of 9 – 2 = 7+.

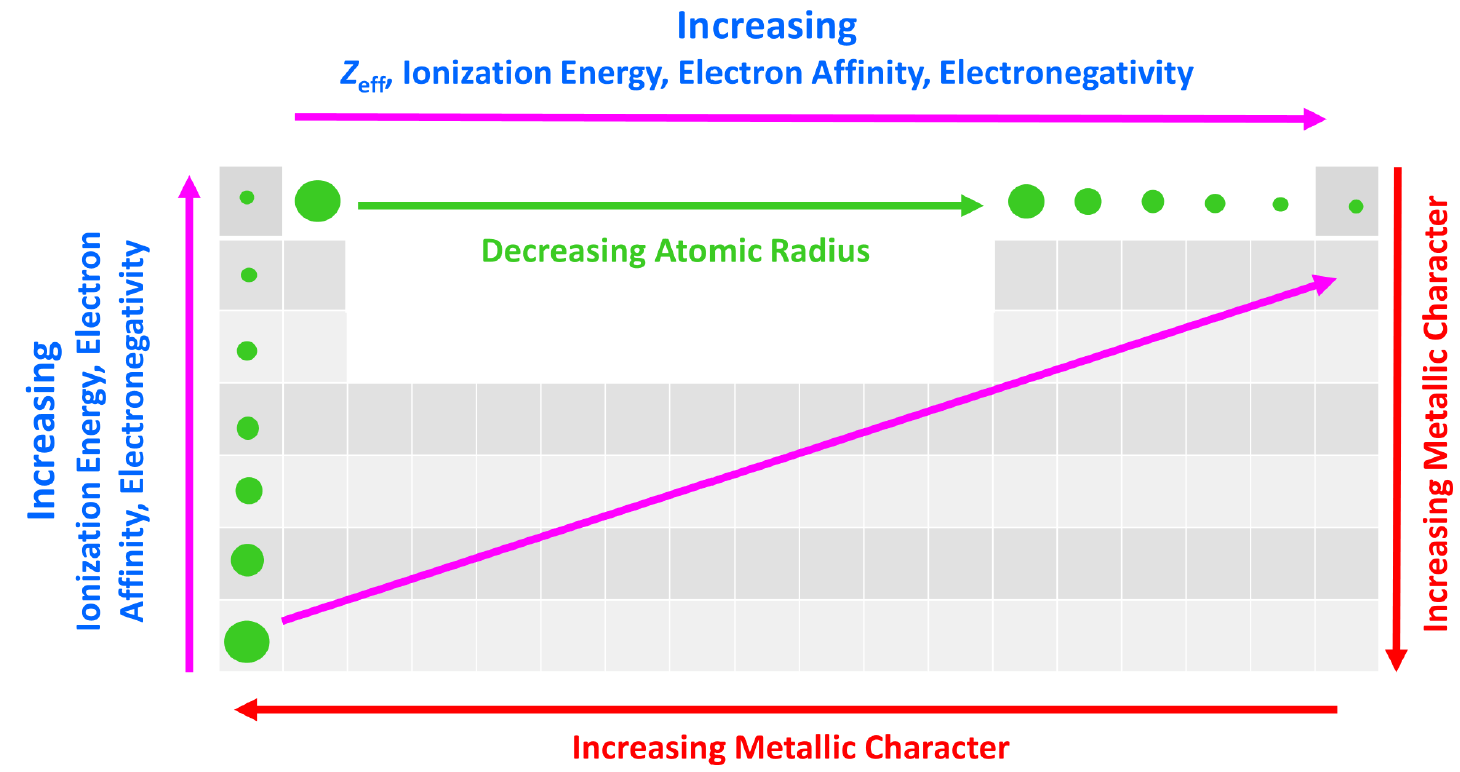
The effective nuclear charge is responsible for many properties of the elements such as electronegativity, ionization energy, atomic radius, etc. The stronger the effective nuclear charge, the smaller the atom and thus the stronger the attractive forces between the nucleus and the valence electrons which means the higher the ionization energies, electron affinity, and electronegativity.

We can put together a general trend for the atomic radius, effective nuclear charge, ionization energy, electron affinity, and electronegativity.

You can look at these as how much an atom ‘likes’ electrons. The more we move to the right in the periodic table, the more the atoms like electrons, because of a greater nuclear charge which increases the ionization energy, electron affinity, and electronegativity. This results in smaller atoms because the nucleus holds the electrons closer and tighter.

This, in turn, means that the metallic character of the elements decreases as metals ‘don’t like’ electrons and tend to become cations.

Check this 95-question, Multiple-Choice Quiz on the Electronic Structure of Atoms including questions on properties of light such as wavelength, frequency, energy, quantum numbers, atomic orbitals, electron configurations, and more.

Free