First order rate law liner equation graph

General Chemistry

In the previous post, we talked about the integrated rate law and its use for determining the concentration of a reactant at a given time when the reaction order was provided.

 

Now, there are questions where the reaction order needs to be determined using the data on how the concentration changes with time.

 

For example,

Given the following kinetics data, determine the order of the reaction, the rate constant, and predict the concentration of A at 450. s.

A → B + C

 

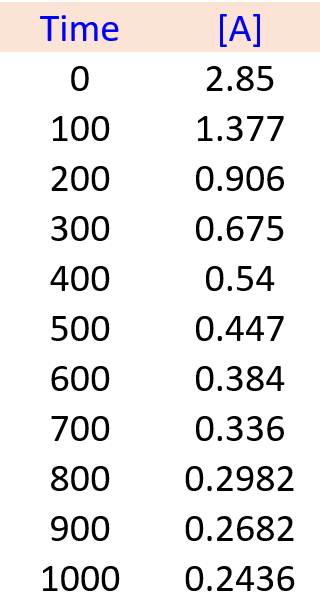
To solve these types of problems, you first need to remember which plot of concentration vs time gives a straight line for the zero-, first-, and second-order reactions:

 

 

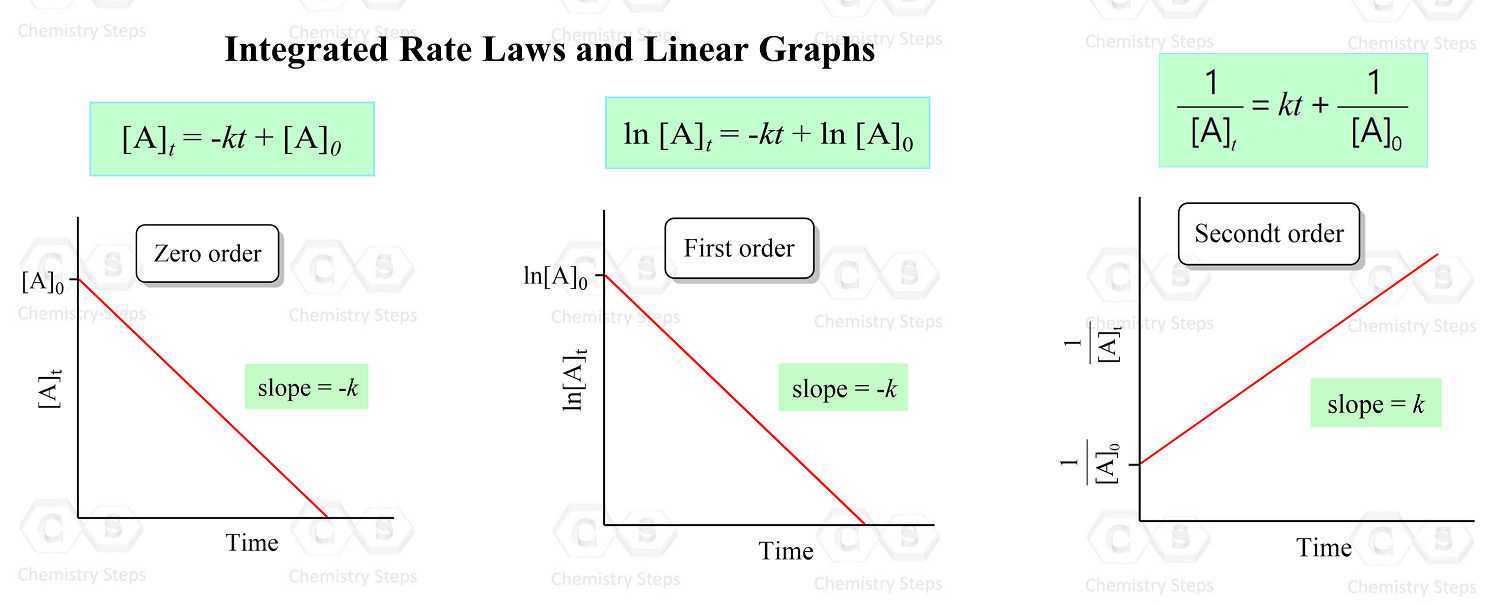
So, the strategy is to plot the data given in the problem and see whether the [A], ln[A], or 1/[A] gives a straight line:

 

 

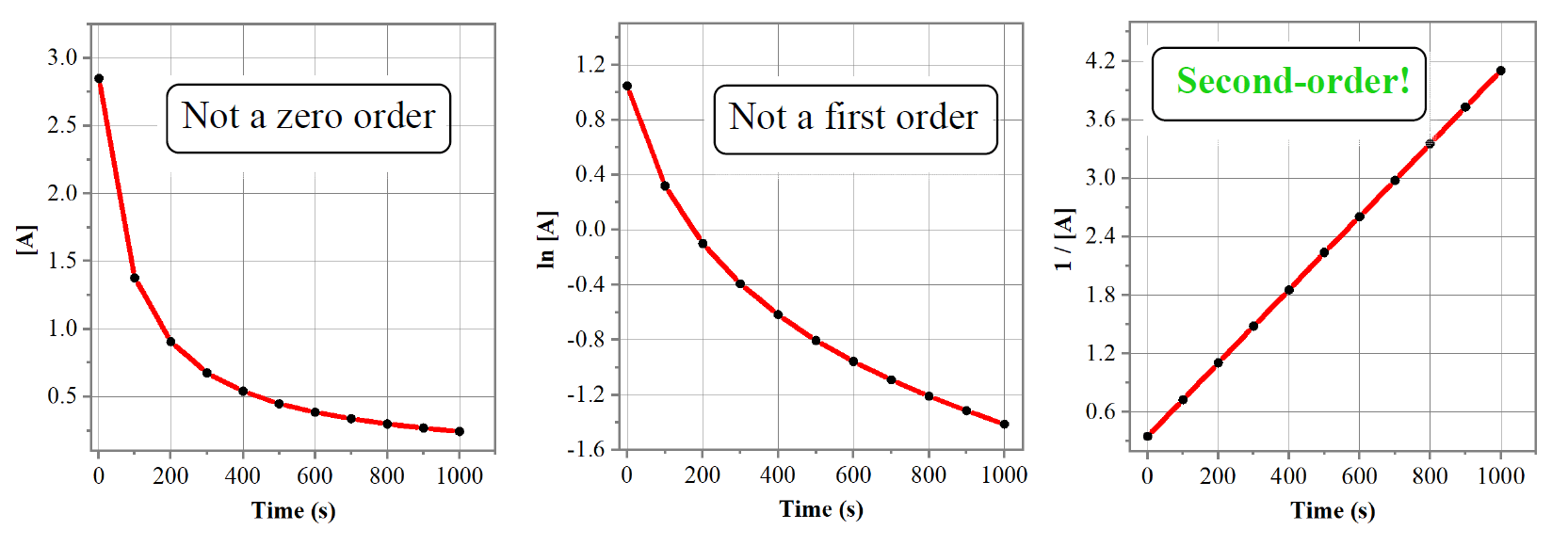
A straight line is obtained when 1/[A] is plotted vs time, indicating a second-order reaction. I used the Origin program to obtain the graphs above, however, this can be done in excel:

 

\[\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_t}}}\; = \;kt\; + \;\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_0}}}\]

y = mx + b

 

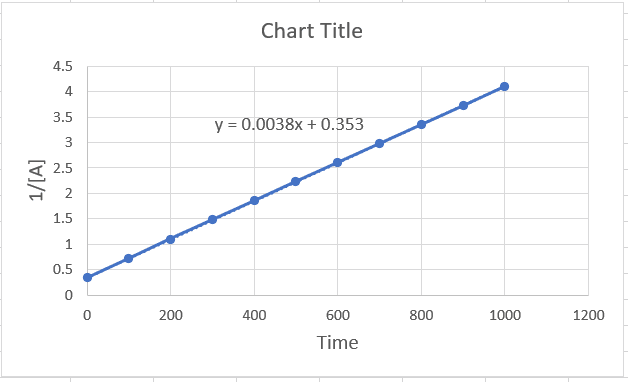
The rate constant is the slope of the graph, which can also be obtained in excel. For this, create the plot 1/[A] vs time, and once it is ready, double click on the graph line > choose “linear” under the format templates on the right > check the box for “Display equation on chart”.

According to excel, k = 0.0038, and because it is a second-order reaction, the units of k are M-1 ⋅ s-1.

Alternatively, the rate constant can be calculated by Δy/Δx (rise/run). So, let’s see how the values of k compare when calculated using these two methods. We can pick any two y and two x values from the graph. Let’s do this for the time interval 200-600 s, since it is relatively easy to see the y values for these points. When x = 200, y = 1.1, when x = 600, y = 2.6. The rate constant then is:

 

k = (2.6-1.1)/(600-200) = 0.00375, which is very close to the value in excel.

 

So far, we have answered two questions: a) The reaction is second order, b) k = 0.0038 M-1 ⋅ s-1

 

Now that we know the value of rate constant, we can calculate the concentration of A at 450. s., by using integrated rate law for second-order reactions:

 

\[\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_t}}}\; = \;kt\; + \;\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_0}}}\]

 

\[\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_t}}}\; = \;{\rm{0}}{\rm{.0038}}\;{{\rm{M}}^{{\rm{ – 1}}}}{{\rm{s}}^{{\rm{ – 1}}}}\;{\rm{ \times }}\;{\rm{450}}{\rm{.}}\;{\rm{s}}\;{\rm{ + }}\;\frac{{\rm{1}}}{{{\rm{2}}{\rm{.85}}\;{\rm{M}}}}\]

 

[A]t = 0.485 M

 

This number makes sense, because according to the table given in the problem, the concentration of A at 400 s is 0.54 M, and at 500 s, it is 0.447 M. So, at 450 s, the concentration must be between 0.54 M and 0.447 M.

 

Here is a 77-question, Multiple-Choice Quiz on Chemical Kinetics:

 

Check Also

 

 

 

Leave a Comment